分层抽样的L层由L-1个分界点所决定，所以最佳分层便是找到L-1个分界点Y′1，Y′2，…，Y′L-1，以使分层抽样的抽样方差在抽样方式、层数和样本量分配方式都为一定时达到最小。

在比例分配中（设fpc可忽略），能使方差

为极小值的一组点也是使

为极小值的最佳分界点。可以证明，满足该条件的第h和h+1层的最佳分界点为

同理可得，在最优分配的条件下，求第h和h+1层的最佳分界点Y′h的方程为(www.daowen.com)

然而，上述方程在实际中是无法求解的，因为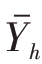 和Sh都与Yh′有关。因此，一些学者曾讨论提出过相关的近似求法，如戴伦纽斯（Dalenius）和霍奇斯（Hodges）1959年提出的快速近似法，塞蒂（Sethi）1963年提出的结合总体分布特征求解的方法等。上述研究都是假定可以用调查变量Y本身的值来分层，而这是不现实的。实际中，常是用某些其他与调查变量Y高度相关的辅助变量X来分层的。研究表明：如果Y和X有直线关系，则用比例分配按X求得的最佳分界点对Y也为最佳；更进一步，如果Y与X的回归是线性的，所有各层中的Y与X高度相关，则用X分层同用Y一样有效。

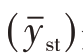设Y=α+βX+e，其中E(e)=0对一切X和e成立，且e与X不相关。是在第h层内e的方差，则使V 达到最小值的Xh′界限满足下列方程：

其中，，ρh是h层内Y与X的相关系数。