（一）估计总体均值的情形

设允许估计量的最大方差为V，对某种已确定的样本量分配原则，有

将nh代入总体均值估计量的方差的计算公式，则有

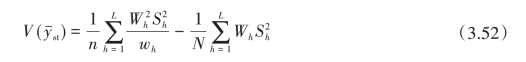
于是对给定的V，可得

当wh=Wh（比例分配）时

当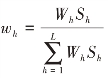（内曼分配）时

当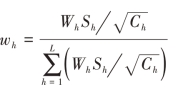（一般最优分配）时

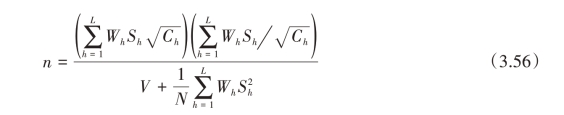
当各层抽样费用不同，而总费用给定时

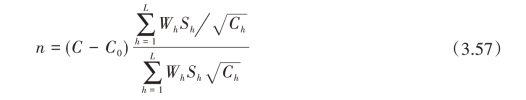
（二）估计总体总值的情形

同样的道理，可得出对给定样本量的分配形式（nh＝nwh）有

当比例分配时

当内曼分配时

当一般最优分配时

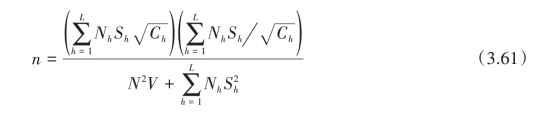
（三）估计总体比例的情形

若Nh较大，则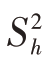≈Ph(1-Ph)，在估计总体比例P时，对给定的样本量的分配形式（nh=nwh）有

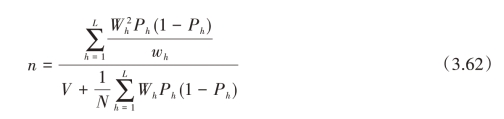(www.daowen.com)

当比例分配时，wh=Wh，有

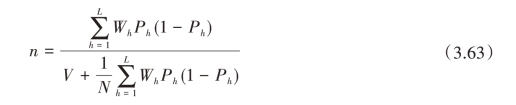
当内曼分配时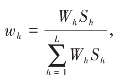，有

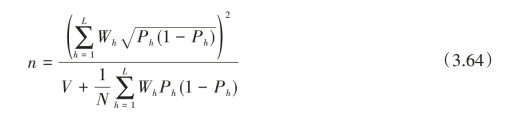
当一般最优分配时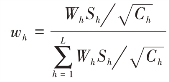，有

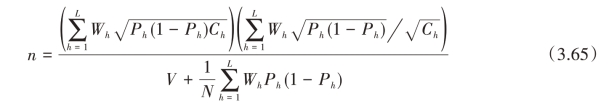
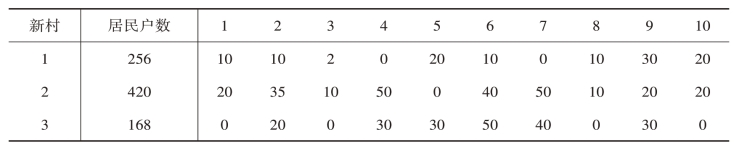
例3.5　某居委会辖有三个居民新村，居委会欲对居民购买福利彩票的情况进行调查，调查者考虑以新村分层，在每个新村中随机抽取了10个居民户，并调查每户最近一个月购买福利彩票所花费的金额（元），表3-6是每个新村及调查的情况。

（1）试估计该居委会居民购买福利彩票的平均支出，并给出估计的标准差。

（2）当置信度为95%，要求极限相对误差不超过10%时，求按比例分配和内曼分配时总样本量及各层的样本量；若三个新村中每户的调查费用分别为c1=9，c2=16，c3=25，求按一般最优分配时总样本量及各层的样本量。

表3-6　每个新村的调查结果

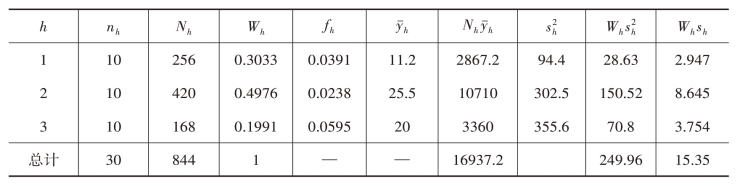
解：根据表3-6中调查数据，计算可得表3-7。

表3-7　根据调查数据计算所得相关统计量的值

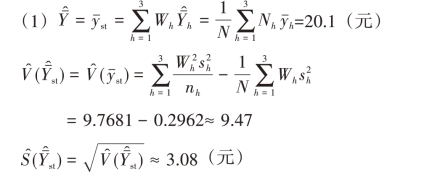
（2）置信度为95%，相对误差为10%，则有

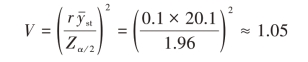
按比例分配时，wh=Wh，总样本量

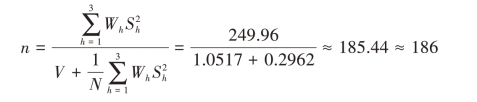
进一步可得各层样本量的分配，n1=nW1≈56，n2=nW2≈93，n3=nW3≈37。

按内曼分配时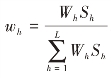，，可得w1=0.1919，w2=0.5636，w3=0.2445，则总样本量

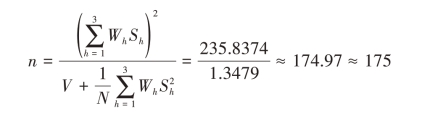
进一步可得各层样本量的分配，n1=n⋅w1≈33，n2=n⋅w2≈99，n3=n⋅w3≈43。

按一般最优分配时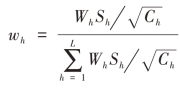，，可　得w1=0.2522，w2=0.5550，w3=0.1928，则总样本量

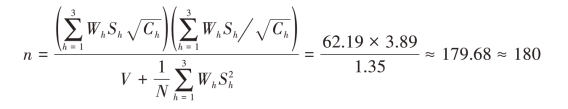
进一步可得各层样本量的分配，n1=n⋅w1≈45，n2=n⋅w2≈100，n3=n⋅w3≈35。

综上所述，按比例分配时，总样本量至少为186，按内曼分配时，总样本量至少为175，按一般最优分配时，总样本量至少为180。