若抽样比f=n/N较大,而个别层的Sh也很大,则按最优分配,一些层的nh有可能超过Nh(即fh>1)。这时,可以对这些极端层进行100%抽样。然后将剩下的其余的层可用的样本量再按最优分配法在其他各层间重新进行分配。以内曼分配为例,其具体步骤如下:
假定n1>N1,则令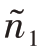 =N1。对n-N1部分作内曼分配
=N1。对n-N1部分作内曼分配

此时,若所有的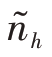 ≤Nh(h≥2),则分配合理。否则,若
≤Nh(h≥2),则分配合理。否则,若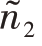 >N2,则
>N2,则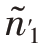 =N1,
=N1,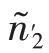 =N2,对n-N1-N2部分再作内曼分配
=N2,对n-N1-N2部分再作内曼分配
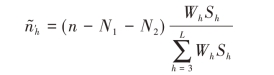
若所有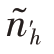 ≤Nh(h≥3),则分配合理。否则再重复上述过程,直到所有的
≤Nh(h≥3),则分配合理。否则再重复上述过程,直到所有的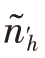 ≤
≤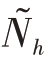 为止。
为止。
此时,最优分配所达到的估计量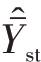 的最小方差公式也应修正为
的最小方差公式也应修正为
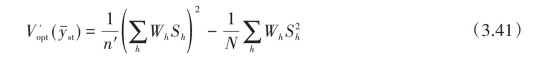
其中,![]() 为仅对
为仅对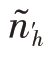 <Nh的层求和,n′为修正后这些层的抽样单元数。这里我们不去证明式(3.41),但是可以直观地理解一下它的含义,因为对于那些实施普查的层(
<Nh的层求和,n′为修正后这些层的抽样单元数。这里我们不去证明式(3.41),但是可以直观地理解一下它的含义,因为对于那些实施普查的层(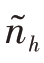 =Nh)来说,已经不存在所谓的抽样误差了,抽样误差只与进行抽样的(
=Nh)来说,已经不存在所谓的抽样误差了,抽样误差只与进行抽样的(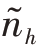 <Nh)层有关。
<Nh)层有关。
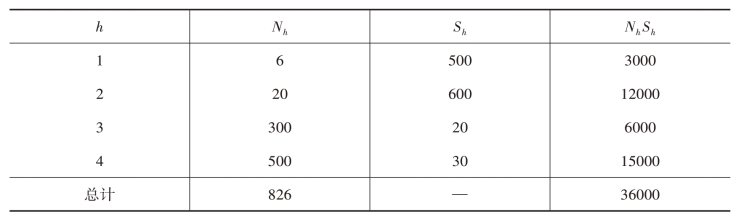
例3.4 假设某个模拟的总体分为四层,Nh和Sh的值列于表3-5中,假定样本量n=100,该如何进行内曼最优分配?
解:第一步:根据表3-5的数据计算内曼最优分配下各层的样本量。
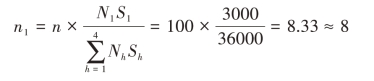
而N1=6,可见n1>N1,因此,令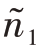 =N1=6。(https://www.daowen.com)
=N1=6。(https://www.daowen.com)
表3-5 一个模拟总体的分层情况
第二步:将n-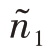 =94个待分配的样本量再按照内曼最优分配的原则分配到第2层到第4层。则
=94个待分配的样本量再按照内曼最优分配的原则分配到第2层到第4层。则
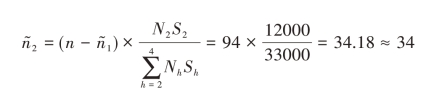
而N2=20,可见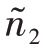 >N2,因此,令
>N2,因此,令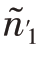 =N1=6,
=N1=6,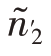 =N2=20。
=N2=20。
第三步:将n-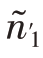 -
-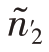 =74个待分配的样本量按照内曼最优分配的原则分配到第3层和第4层。则
=74个待分配的样本量按照内曼最优分配的原则分配到第3层和第4层。则
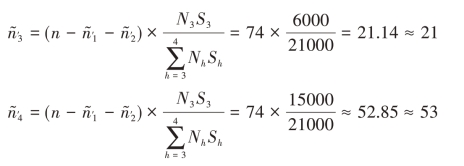
而N3=300,N4=400,满足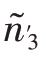 <N3,
<N3,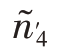 <N4。
<N4。
第四步:确定各层最终所分配的样本量。
![]()
第五步:根据式(3.41)计算此时总体均值估计量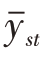 的最小方差
的最小方差
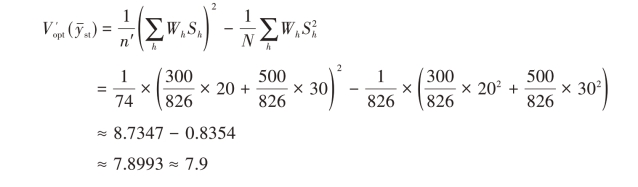
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






