（一）一般情形

在分层随机抽样中，在给定费用条件下，使估计量的方差达到最小，或在精度要求（常用方差表示）一定条件下，使总费用最小的各层样本量的分配称为最优分配。

在分层随机抽样中，费用函数可能是简单线性的，也可能是其他复杂形式，这里主要考虑简单线性的费用函数

其中，C0是固定费用，如组织宣传费、分层及编制抽样框的费用等，Ch是在第h层抽取一个单元的平均费用，包括调查员报酬、旅差费、调查测试费等。

根据前面的论述，在估计总体均值时，对给定的各层样本量nh，估计量的方差可表示为

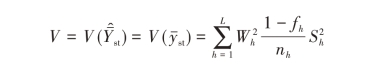
即

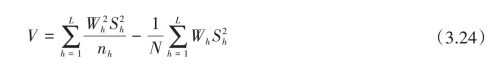
可见，式（3.24）中第二项与样本量无关。进一步可得

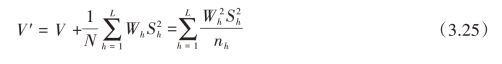
考虑到

则

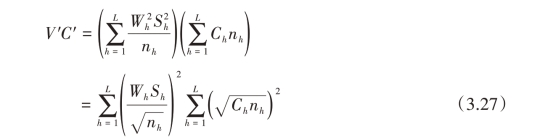
所以，在给定总费用C下使估计量的方差V最小与在给定V下使费用C最小，均等价于使V′C′达到极小值。

根据柯西—施瓦兹（Cauchy-Schwarz）不等式，有

其中，等号只有在以下情形时才成立（V′C′达到极小值）：

这意味着

则

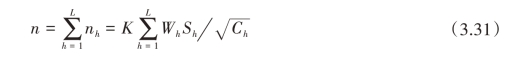
因此

所以，使V′C′达到极小值的最优分配即为

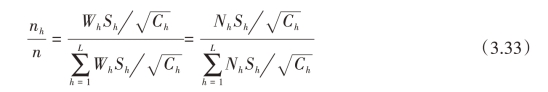
即(www.daowen.com)

可见，最优分配的结果既考虑了总体各层的差异，同时也考虑了总体各层内变异程度的差异和各层内平均调查费用的差异。当层的容量越大、层内变异程度越大，层内每调查一个单元的费用越小，则在该层中抽取的单元数应越多。

（二）特殊情形——内曼分配

如果各层内每个单元的平均抽样费用相等，即C1=C2=…=Ch时，最优分配简化为

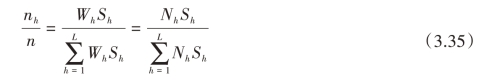
即

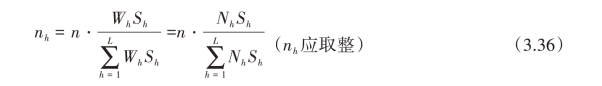
这个结果称为内曼（Neyman）分配。因为最先人们认为它是由内曼于1934年给出的，实际上后来才发现早在1923年它已被俄国学者楚波罗（Tschuprow）给出。

在内曼分配时，估计量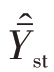所能达到的最小方差为

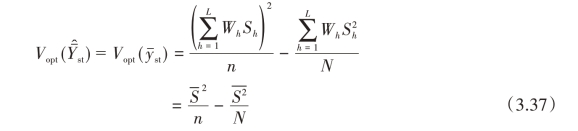
其中，，为各层标准差Sh按层权的加权平均，为各层内方差按层权的加权平均。有时也用Vmin来表示这里的Vopt。

（三）估计总体比例P时的最优分配

1.一般情形

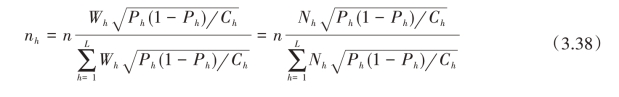
2.特殊情形——内曼分配

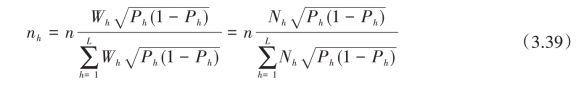
在实际工作中，由于Sh或Ph(1-Ph)未知，需根据有关信息进行估计，以致使实际的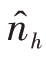同最优分配时的nh相比会产生一些偏误，进而使估计量的精度会受到影响，但从分析比较的结果看，这种影响不会太大。

例3.3　某市有甲、乙两个地区，现要进行家庭收入的调查。令n=500，已知甲地区共有20000户居民，乙地区共有50000户居民；甲地和乙地每户的平均抽样费用比为2∶3，请分别计算出在甲地和乙地进行比例分配、一般最优分配（考虑费用因素）以及内曼分配（不考虑费用因素）的样本量。

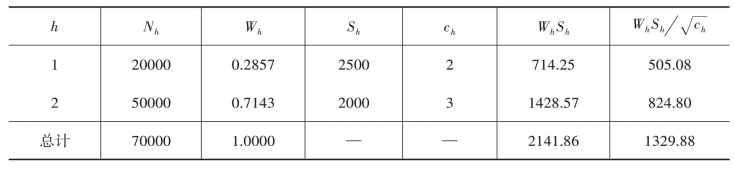
解：根据已知数据，通过计算整理可得表3-4。

表3-4　关于计算样本量分配的相关统计量

（1）比例分配

n1=nW1=500×0.2857=142.86≈143

n2=nW2=500×0.7143=357.14≈357

（2）一般最优分配

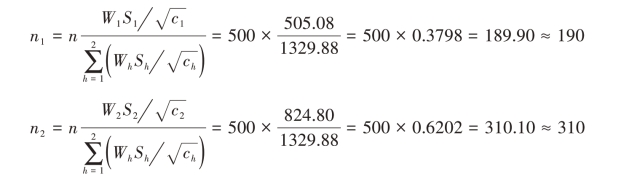
（3）内曼分配

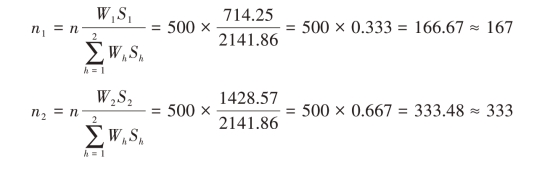
比较三种分配方法的结果可以发现，一般最优分配在乙地所分配的样本量最小。这是因为一般最优分配考虑了费用的因素，在乙地抽样的单位平均费用较高，所以最优的分配原则应适当增加甲地的样本量，减少乙地的样本量。