(一)总体均值估计量的方差
对于一般的分层抽样,由于各层的抽样是相互独立的,诸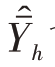 也相互独立,因此总体均值
也相互独立,因此总体均值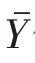 估计量的方差是总体各层均值估计量方差的加权平均,即
估计量的方差是总体各层均值估计量方差的加权平均,即
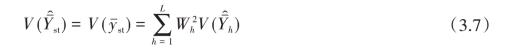
式中V  是第h层总体均值估计量的方差。
是第h层总体均值估计量的方差。
对于分层随机抽样,则有
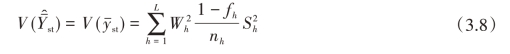
可见,在分层抽样中,总体均值估计量的方差只与各层内的方差有关,而与层间方差无关。而总体方差又是由层内方差与层间方差两部分构成的,所以,估计量的方差小于总体方差。
(二)总体总值估计量的方差
有了总体均值估计量的方差,可推导出总体总值估计量的方差
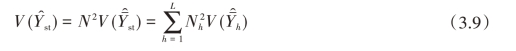
对于分层随机抽样,则有

(三)总体比例估计量的方差
估计总体比例,当Nh充分大时,有

对于分层随机抽样,则有
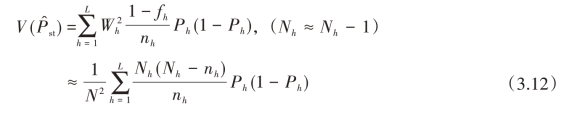
四、简单估计量方差的估计量
按上述方法确定估计量的方差时,要求各层的总体方差应事先已知,但实际工作中,各层的总体方差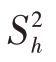 又常常是未知的,一般可用对应的各层样本方差
又常常是未知的,一般可用对应的各层样本方差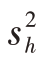 替代,对估计量的方差作出估计。
替代,对估计量的方差作出估计。
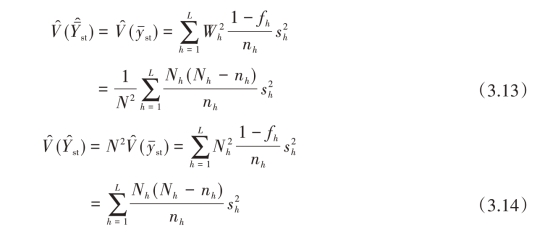
且,![]() 与
与![]() 分别是
分别是![]() 与V无偏估计。
与V无偏估计。
当用样本资料估计方差V![]() 时,可将
时,可将![]() 用
用![]() 替代,则得
替代,则得
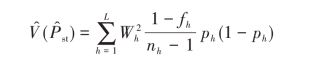
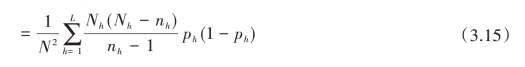
且![]() 是V
是V![]() 的无偏估计。
的无偏估计。
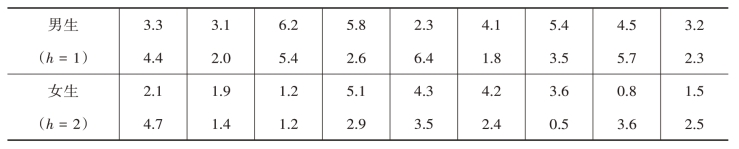
例3.1 (续例2.1)在例2.1中,已知该专业有男生660名,女生540名,为了方便调查,采用分男生、女生的分层随机抽样抽得36名学生进行调查,调查数据如表3-1所示(单位:小时)。试估计该专业大学生每天平均上网时间,并求出95%置信水平下的置信区间。
表3-1 分层随机抽样调查36名学生每天上网时间
 (https://www.daowen.com)
(https://www.daowen.com)
解:由题意及表3-1数据可知,N=1200,N1=660,N2=540,nh=18(h=1,2),各层的层权及抽样比为:
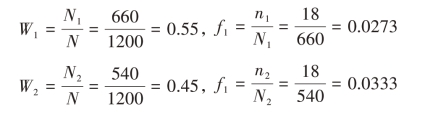
各层样本均值及样本方差为:

估计该专业学生每天平均上网时间为
![]()
估计量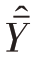 ̂的方差及标准差的样本估计为
̂的方差及标准差的样本估计为
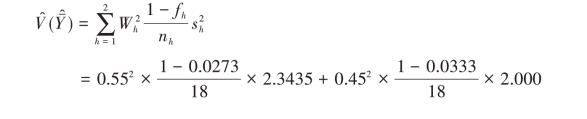
![]()
则![]()
故该专业大学生每天平均上网时间在95%置信水平下的置信区间估计为
![]()
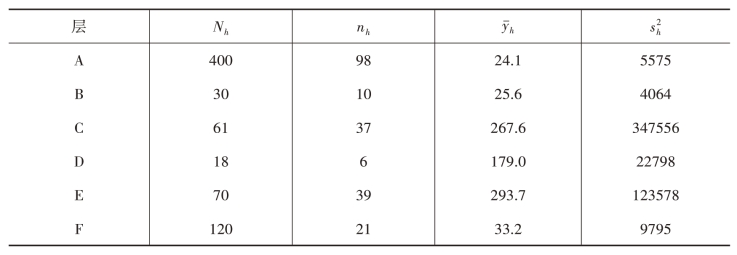
例3.2 Sniff和Skoog(1964)于2025年2月采用分层随机抽样估计阿拉斯加州北美驯鹿Nelchina种群的数量,在1月和2月对一些抽样技术进行了实地测试。实地测试表明,几种设想的抽样单元(如等时间间隔的抽样单元)是难于操作实施的,而4平方英里的等区域抽样单元对于调查更为合适。生物学家根据先前对北美驯鹿密度的估计数据将目标地区划分为6层;在每一层内再将土地划分为4平方英里大小的方格作为抽样单元。例如在A层中包含了N1=400个抽样单元,调查时从中随机选取了n1=98个单元。报告的数据如表3-2所示。
表3-2 样本相关数据
资料来源:Sharon L.Lohr著,金勇进编译的《抽样:设计与分析》,中国统计出版社,2009。
解:根据表3-2数据,计算执行分层抽样所需的数据如表3-3所示。
表3-3 计算所得相关统计量的值
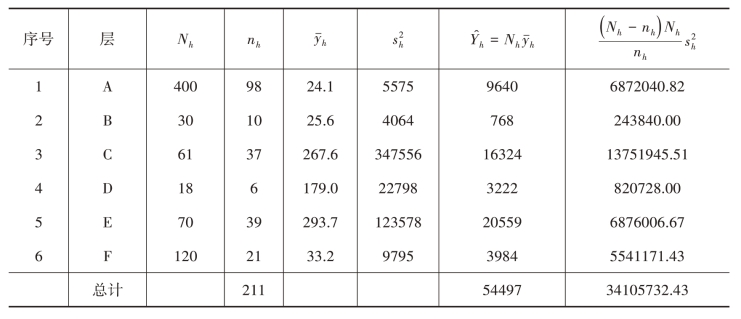
总体总值的估计量为

估计量的方差估计为
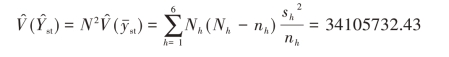
则,![]()
故北美驯鹿总数量的估计值是54497只、标准差为5840只。北美驯鹿总数量的95%置信区间近似为
![]()
当然这个置信区间只是反映由抽样误差造成的不确定性,如果在实地调查中漏计了北美驯鹿的数量,那么整个置信区间将会是偏低的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





