在简单随机抽样中，样本均值是总体均值的无偏估计。在分层抽样中，若仍用样本均值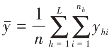来估计总体均值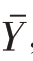，在一般情况下是否合理？先看下面的引例。

引例　总体由1000人组成，按以往收入情况分成两层，第一层（收入较高层）20人；第二层（收入较低层）980人。从第一层随机抽2人，调查上月收入得12000和16000元；从第二层抽8人，上月收入分别为2200、2300、1800、3200、4000、3400、2800及3600元。估计这1000人的月收入。

如果用样本均值

估计总体平均值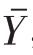，显然偏高。

若先分别算出这两层的样本均值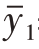=14000元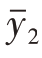，=2912.5元，则用

估计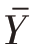就合理多了。由此，分层抽样的估计量可按如下方式来构造。

（一）总体均值的简单估计量

在分层抽样中，总体均值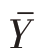的估计量一般用样本均值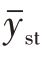表示，它是各层总体均值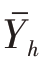的估计量按层权Wh的加权平均，即

一般情况下

在分层随机抽样中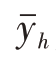，是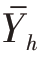的无偏估计量，即E 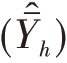=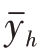，因此，(www.daowen.com)

且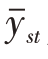是的无偏估计量。

（二）总体总值Y的估计量

由总体均值的估计量，可推出总体总值的估计量

（三）总体比例P的估计量

若令

则

按照总体均值估计量的公式，可推出总体比例（成数）P的估计量为

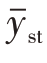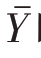可以证明，在分层随机抽样中，是的无偏估计量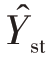，是Y的无偏估计量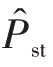，是P的无偏估计量。