运用精度要求来确定样本容量时，必须事先知道总体的方差。但在调查之前总体特征是未知的，所以要对总体特征（总体均值及方差）进行预估计。预估计总体方差的方法一般有以下几种：

（1）两步抽样法。即在正式开展抽样调查工作之前，先从总体中抽取一个容量为n1的简单随机样本，求得S2的估计值或P的估计值，把n1和（或n1和）代入相应的公式计算所需的n，然后，再补抽其余的n-n1个单元进行正式调查。

考克斯（Cox）1952年在斯坦（Stein）工作的基础上提出了在给定的精度下求n的公式（假定n1≤n，n1足够大时，使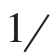n1可忽略，又fpc也可忽略）。

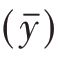①估计时，若要求V =V =V，则

②估计P时，若要求V 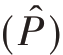=V，则

第二步抽样后，从总的容量为n的样本给出的估计是有偏的，应取

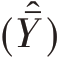③估计时，若要求标志变异系数C =C =（假定Yi服从正态分布），则

所得的是有偏的，取̂=(1-2C)。(www.daowen.com)

④估计P时，若要求标志变异系数C =C(p)=，则

第二步抽样后，从总的容量为n的样本给出的估计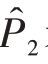是有偏的，应加以修正。取

（2）对于一次性的调查，采取在正式调查前进行试点调查，根据试点调查的结果估计S2或P。试点调查的目的是多方面的，不只是估计S2或P，若试点调查是通过简单随机样本进行的，就可用上面的方法。但试点调查的对象往往有选择性，用其结果来估计S2时，可能偏低。

（3）对于经常性调查项目，可以利用以前调查的结果，也可对以前调查的结果做适当调整。一般情况下，如果以前的调查结果有若干个时，常选择其中最大的方差来确定样本容量，从而保证充分满足估计精度的要求。

（4）根据总体的结构，应用数学方法预测总体方差S2或P。如对正态分布总体，可用标准差与全距间的关系来定出总体方差；对均匀分布、泊松分布总体也可以用有关数理统计的知识来确定出总体方差。

（5）估计比例时，可借助某些基本信息、方法或经验等。如估计总体比例大约在0.3～0.7之间时，可以直接取比例方差的最大值0.25来确定样本容量，这通常是一种比较“安全”的选择。但当总体比例估计小于0.1时，对于依不同的总体比例确定的样本容量常常可能相差很大，有时甚至相差10倍以上，因此，在这种情况下，一般采用逆抽样的方法。

逆抽样法是由霍尔丹（Haldane）于1945年提出的一种适用于确定稀有元素抽取样本容量的方法。基本思想：事先确定一个整数m(m＞1)，进行逐个随机抽样，当抽到n个单元中有m个具有所研究属性特征的单元时，终止抽样，此时的n即为实际的样本容量，它是一个随机变量，一般服从负二项分布，即