（一）精度与样本量的关系

精度的概念比较复杂，通常精度由误差来表现。如果不考虑非抽样误差，则精度的具体体现就是抽样误差，用抽样误差（估计量的方差）的倒数表示。抽样误差越小，说明用统计量对总体参数进行估计时的精度就高，反之抽样误差越大，说明估计量的精度就低。在抽样设计中估计量的抽样误差用均方误差MSE ̂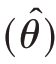表示，若估计量是总体参数的无偏估计，则抽样误差的具体体现就是估计量的方差V 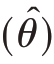。抽样误差与样本量有密切关系，样本量越大，在其他条件相同的情况下，抽样误差就越小，抽样的精度就越高。对于简单随机抽样，如何确定精度与样本容量n的具体关系呢？要回答这一问题，首先分析影响样本容量n的因素有哪些。

从简单估计量的性质出发，容易知道样本容量n的大小会影响抽样误差，因为n如果足够接近N，则抽样误差就会足够接近于零，这一点也清楚地体现在总体均值估计量方差的核心定理的内容中。

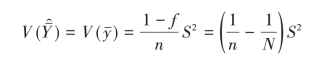
然而从上式中可以解出

进一步可得

由此可见，影响样本容量n的因素有三个：总体容量N，（目标）抽样误差V 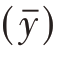和总体方差S2。抽样误差V 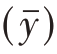越小，样本量n就越大，抽样的精度就越高。

（二）精度的不同表示方法

在一定的可靠程度要求下，给出估计精度，也就等于给出了估计中允许误差的大小。通常，对于估计量的精度可以有不同的提法或表示方法。

提法一：以置信度1-α，允许总体参数θ的估计量θ̂的最大绝对误差为d，即

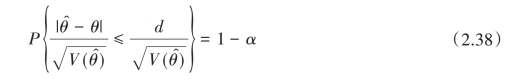
根据双侧百分位点的定义，有

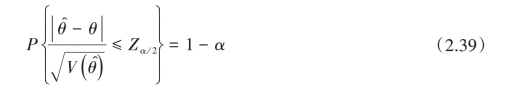
由此可知最大绝对误差可以通过估计量的方差表示，即

提法二：以置信度1-α，允许总体参数θ的估计量̂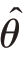的最大相对误差为r，即

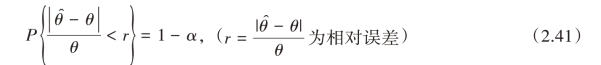
最大相对误差可以通过估计量的变异系数表示，即

所以，d=rθ。

提法三：以置信度1-α，允许总体参数θ的估计量̂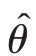的最大方差不超过V，即

提法四：以置信度1-α，允许总体参数θ的估计量̂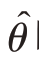的最大变异系数不超过C，即(www.daowen.com)

（三）样本容量n的确定

当n足够大时，可以认为̂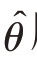服从正态分布N(θ，V 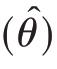)（理由如前述样本统计量的抽样分布）。因此，由上述四种对估计量精确度的不同提法，可以分别得到下列方程式

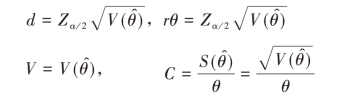
因为V 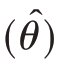是n的函数，求解以上四个方程，即可确定n。

1.估计总体均值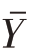时的样本容量n

由于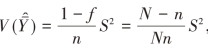，代入上述方程解可得表2-5。

表2-5　不同精度要求下估计总体均值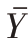时的样本容量n

2.估计总体总值Y时的样本容量n

由于，代入上述四个方程可解得表2-6。

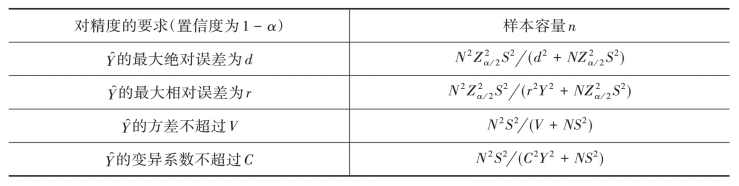
表2-6　不同精度要求下估计总体总值Y时的样本容量n

3.估计总体比例P时的样本容量n

由于，代入上述四个方程可解得表2-7。

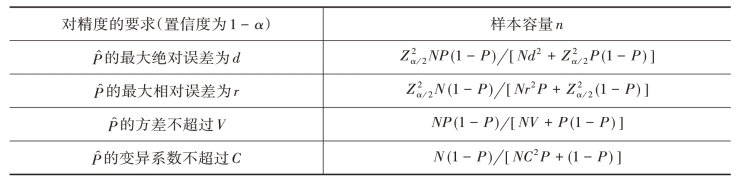
表2-7　不同精度要求下估计总体比例P时的样本容量n

例2.3　（续例2.1）在例2.1中，若要求以95%的置信度保证相对误差不超过10%，样本容量至少是多少？

解：已知N=1200，n=36，α=0.05，r=0.1，根据样本数据计算得：

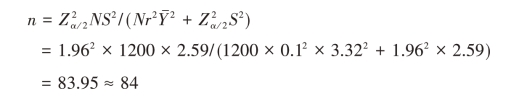
故样本容量至少需要84个。

总体均值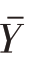和方差S2未知，用例2.1中的样本的均值和方差代替，因为该样本的均值和方差均是总体均值和方差的无偏估计。

例2.4　（续例2.2）在例2.2中，如果小区管理者预计赞成的比例能达到80%，要求估计绝对误差不超过5%，应抽取多少户进行调查？

解：已知N=480，n=50，α=0.05，=1.96，d=0.05，

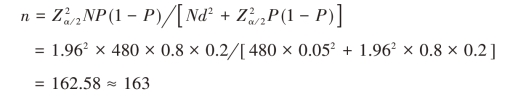
故应抽取163户进行调查。