【摘要】:对于简单随机抽样,可以证明样本方差s2为总体方差S2的无偏估计量,即E=S2,所以,当总体方差S2未知时,可用样本方差s2来代替,由此可得出估计量的方差的估计量分别为而且与分别是V 与V 的无偏估计。采取简单随机抽样方法抽取了50户进行调查,其中有32户赞成,18户反对。
对于简单随机抽样,可以证明样本方差s2为总体方差S2的无偏估计量,即E(s2)=S2,所以,当总体方差S2未知时,可用样本方差s2来代替,由此可得出估计量的方差的估计量分别为
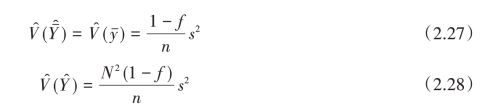
而且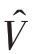
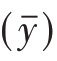 与
与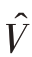
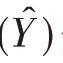 分别是V
分别是V 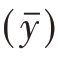 与V
与V 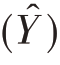 的无偏估计。
的无偏估计。
对总体比例的简单估计量的方差进行估计时,令

有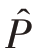 ̂=p=
̂=p=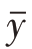 ,则
,则
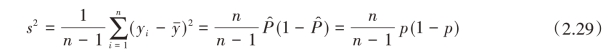
可得总体比例P估计量的方差V 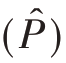 的无偏估计量为
的无偏估计量为
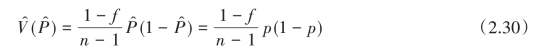
总体中具有某种属性单元总数N1估计量的方差V 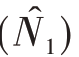 的无偏估计量为
的无偏估计量为
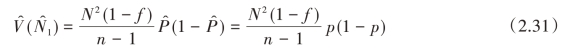
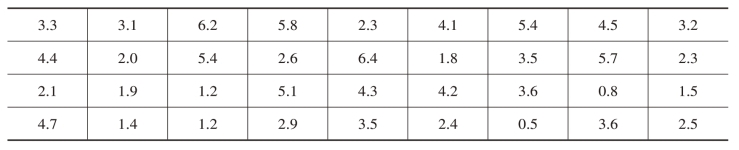
例2.1 某大学某专业共有1200名学生,学生管理工作者为了了解该专业学生每天上网的时间,用简单随机抽样的方法抽取了36名学生,调查每天上网时间,得到如表2-4所示的数据(单位:小时)。试估计该专业学生每天平均上网时间,并求出95%置信水平下的置信区间。
表2-4 抽样调查36名学生每天上网时间(单位:小时)
 (www.daowen.com)
(www.daowen.com)
解:已知N=1200,n=36,![]() ,α=0.05,根据样本数据计算得
,α=0.05,根据样本数据计算得
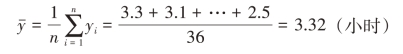
因此,根据样本估计该专业学生每天平均上网时间为3.32小时。
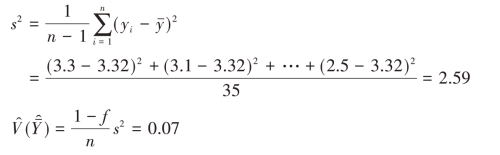
估计量的估计标准差为
![]()
已知分位数![]() =1.96,估计该专业学生每天平均上网时间95%置信水平下的置信区间为
=1.96,估计该专业学生每天平均上网时间95%置信水平下的置信区间为
![]()
例2.2 某居民小区共有居民480户,小区管理者准备采用一套新的供水设施,想了解居民是否赞成。采取简单随机抽样方法抽取了50户进行调查,其中有32户赞成,18户反对。试估计该小区居民中赞成使用新设施的户数比例的置信区间,置信水平为95%。
解:已知N=480,n=50,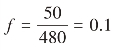 ,
,![]() ,又α=0.05,分位数
,又α=0.05,分位数![]() =1.96。由式(2.30)得
=1.96。由式(2.30)得
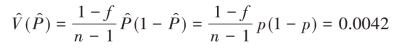
总体中赞成使用新设施的户数比例的95%的置信区间为
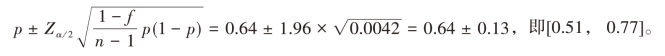
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关抽样调查(修订版)的文章






