在抽样推断中，有时往往只计算出估计量的值，而不大注意估计量的误差（方差或标准差）。但是，总体均值的估计量通常与总体均值的真值间不完全一致，即存在误差，而且所有可能的样本均值相对于总体均值的误差大小也是不一致的。联合国统计局编的《抽样调查理论基础》一书指出：“从研究大多数国家的抽样实践中，可以看出：虽然计算估计量的标准差，至少对关键性的几个估计量计算其标准差来说，仅需增加很少的额外开支或负担，但是他们并没有意识到确定估计量的标准差的重要意义。这是否因为统计人员无意识地忽视了估计量的不精确性所产生的严峻现实呢？计算标准差，并且把他们与估计量一起列出来，应该成为实际工作的一个常规。”

估计量的标准差就是所有可能的样本均值（或比例）对应于总体均值（或比例）的平均误差，即抽样平均误差。其平方即为估计量的方差，常用V表示。

为表达均值估计量的方差，我们先定义总体方差，按一般定义，有限总体的方差为

但为了在大多数情况下使公式的表达更简练，常将总体方差表示为

这种表示方式在用方差分析法处理时尤为方便。

（一）总体均值简单估计量的方差

估计量方差的大小反映估计量精度的高低。估计量方差小，说明估计量（是一个随机变量）的波动小，意味着该估计量的结果稳定，精度高；反之则意味着估计量精度低。

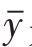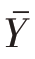定理1　由于样本均值是总体均值的无偏估计量，因此估计量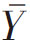的方差为

其中，1-f为有限总体不重复抽样校正系数，记为fpc。

证明：仍引进随机变量(www.daowen.com)

于是根据（2.15）～（2.17）式可得

这个定理俗称抽样理论的核心定理，之所以如此，是因为抽样调查结果的精度（一般用其相反的量——误差表示）高低乃是评价调查成功与否的重要指标。当估计量θ̂恰是抽样中的核心估计量样本均值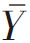时，V(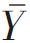)既是精度又是信度的理论表达。

（二）总体总值简单估计量的方差

由总体均值简单估计量的方差进一步可推出

（三）总体比例简单估计量的方差

在研究总体比例时，令

有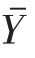=P，则

进一步可得总体比例P估计量的方差为

总体中具有某种属性单元总数N1估计量的方差为