（一）总体均值的简单估计量

在简单随机抽样条件下，以样本均值作为总体均值的简单估计量，即

（二）总体总值的简单估计量

以样本均值的N倍作为总体总值的简单估计量，即

其中，N n也称作膨胀因子。

（三）总体比例的简单估计量

抽样调查中，经常需估计总体中具有某种特征的单元总数及其在总体中所占的比例。

设总体中的N个抽样单元按其是否具有某种特征可分成D和D′两类，D类具有某种特征，D′类不具有某种特征。D类有N1个单元，D′类有N0个单元，如表2-3所示。

表2-3　总体比例与样本比例

令

则总体中属于D类的单元总数

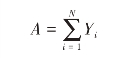
总体中属于D类的单元比例

由此则将估计N1和P的问题转化为估计Y和，所以依上面的结论可知总体比例的简单估计量为(www.daowen.com)

总体中具有D类属性的单位总数N1的估计量为

总体参数简单估计量有如下性质。

性质1对于简单随机抽样，样本均值是总体均值的无偏估计，即

证明：从大小为N的总体中抽取一个样本容量为n的简单随机样本。对总体中的每个单元Yi，引进随机变量ai如下：

则

由（2.15）～（2.17）式可得

其中，Yi (i=1，2，…，N)都是常数，故

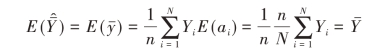
性质2对于简单随机抽样，̂=N 是总体总值的无偏估计，即

性质3对于简单随机抽样，样本比例是总体比例的无偏估计，即