由于抽样指标是一个随机变量，随着抽取的样本不同，便有不同的估计值，因此，要判断一种估计量的好坏，仅从某一次试验的结果来衡量是不够的，而应从多次重复试验中看这种估计量是否在某种意义上最接近于被估计参数的真值。一般来说，用抽样指标估计总体指标应该有三项基本要求或标准，满足这三项要求的估计就可以被认为是合理的估计或优良的估计，这三项要求即是抽样估计的三条优良标准。

（1）无偏性。用样本指标估计总体指标要求所有可能的样本指标的平均值等于对应的总体指标值。就是说，虽然每一次的抽样指标和未知的总体指标可能有偏误，但在多次反复的估计中各个抽样指标的平均值应该等于总体指标，即用抽样指标进行估计，平均来说是没有偏误的。所以，样本指标是对应的总体指标的无偏估计量。关于这一点，可以用概率的方法加以证明。

证明：设总体有N个单元：Y1，Y2，…，YN，则总体均值

又设样本有n个单元，观测值为y1，y2，…，yn，则样本均值

所以

由于y1，y2，…，yn都是取自总体Y1，Y2，…，YN中，当n充分大时，它与总体同分布，则E(y1)=E(y2)=…=E(yn)=E(Yi)=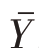，因此

（2）一致性。即用样本指标估计总体指标，要求当样本容量充分大时，抽样指标也充分地靠近总体指标。换言之，随着样本单元数n的无限增大（无限接近于总体单元数N），抽样指标和总体指标间的绝对离差可以无限缩小。

以样本均值为例，设ε为任意小的正数，依大数定律有(www.daowen.com)

由平均数无偏性知道，样本均值的期望值等于总体均值，即E 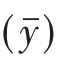=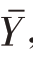，则有

这表明，当样本单位数无限增大时，样本均值和总体均值的绝对离差小于任意常数ε（ε＞0）的概率趋近于1。这就是抽样估计的一致性。

（3）有效性。用抽样指标估计总体指标，要求作为优良估计量的方差应该比其他估计量的方差小。即用样本均值和总体另一指标来估计总体均值，虽然两者都是无偏估计量，而且在每一次的估计中两种估计量和总体均值都可能有离差，但样本均值更靠近在总体均值的周围，平均说来它的离差比较小，所以对比而言，样本均值是更为优良的估计量。

由于样本变量和总体变量是同分布的，依方差性质可知

故V 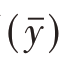＜σ2，所以用样本均值估计总体均值比用总体的变量Yi估计总体均值更为有效。

要达到对总体的正确认识，样本的充分代表性和样本资料的准确性是必要的前提，从样本到总体的估计方法在抽样调查中居于重要地位。抽样估计就是以样本的实际资料为依据，计算一定的样本统计量，并按照一定的方法对总体参数作出估计和推断，这也是抽样调查的目的之所在。