抽样估计就是以样本统计量来估计未知的总体参数。

如果以估计中所依据的资料不同来区分，一般可以有简单估计、比率估计和回归估计等三种方法。

简单估计是单纯依靠样本调查变量的资料估计总体参数，其估计结果称为简单估计量；比率估计和回归估计是同时依据样本调查变量以及已知的有关辅助变量的资料来对总体参数做出估计，其结果分别称为比率估计量和回归估计量。简单估计是最简单、最基本的一种估计方法，在实际中应用也最为广泛。后面各章节所讨论的估计量若没有特别的说明一般都是指简单估计量。同简单估计相比，比率估计和回归估计比较复杂，但在某些情况下，其估计的效果却比较好。

如果以估计结果的表示方式来区分，则抽样估计可以有两种形式，即点估计和区间估计。

点估计是指给所要估计的总体参数只给出一个明确的估计点值，同时确定出估计结果的误差，一般用方差V ̂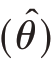来表示。

区间估计则是在一定的概率保证程度（置信度）之下，根据允许的最大绝对误差范围，确定出一个以点估计值̂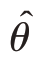为中心的区间作为总体待估参数θ的估计区间，也称为置信区间。一般来说，若估计量̂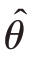是无偏的，且呈正态分布，则参数θ的置信度为1-α的置信区间可以写成

当调查变量的总体方差σ2已知时，上述置信区间可表示为

(www.daowen.com)

即取K=，的值可以通过查正态分布双侧临界值表加以确定。常用的几组置信度与的对应值如表1-5。

表1-5　常用置信度与的对应值

当调查变量的总体方差σ2未知时，则用相应的样本方差s2代替。然而，这时有可能会使误差产生一个增量，特别是当样本较小时，更容易影响估计的精度。因此，为了保持1-α的置信度，就应该适当加宽置信区间，即用较大的值来代替。此时，置信区间就可以表示成

其中，的值可通过查t分布临界值表来确定，自由度为df=n-1，n为样本容量；表示以s2代替σ2后对抽样标准误S ̂的估计量。

注意到，当样本容量充分大时，Z值和t值十分接近，因此，即使σ2未知，也仍然可以取K=Z；但在小样本条件下，Z值和t值差别较大。所以，在实践中，只有当σ2未知且样本容量较小（n＜30）时才用t值，即取K=t。

可见，在区间估计中，不但要考虑抽样误差的可能范围有多大，而且还必须考虑落到这一范围的概率是多少。前者是估计的准确性问题，后者是估计的可靠性问题，两者既相互矛盾又密不可分。计算可靠性的依据是样本统计量的抽样分布理论。在实际问题的研究中常常需要在估计的准确性和可靠性之间进行协调，一般是先确定其中的一个，然后再推算出另外一个。