由于从一个总体中抽取样本容量为n的样本时,有多种可能的结果,所以样本指标是随机变量,而总体指标是唯一确定的常量,故抽样误差也是一个随机变量。
设θ为总体的某个待估参数,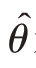 ̂是通过样本资料计算而得到的关于θ的估计量,则估计的实际误差为
̂是通过样本资料计算而得到的关于θ的估计量,则估计的实际误差为 ̂-θ,由于θ未知,故
̂-θ,由于θ未知,故 ̂-θ是未知的。这表明根据某一个确定的样本,无法确定抽样误差的大小,因此,关于抽样误差的计算,是建立在误差分布理论基础上从统计平均意义角度来考虑的。因为,对一个确定的总体按同一种抽样方法可能得到一系列不同的样本,对每一个样本都会有一个估计的实际误差
̂-θ是未知的。这表明根据某一个确定的样本,无法确定抽样误差的大小,因此,关于抽样误差的计算,是建立在误差分布理论基础上从统计平均意义角度来考虑的。因为,对一个确定的总体按同一种抽样方法可能得到一系列不同的样本,对每一个样本都会有一个估计的实际误差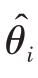 ̂-θ,所以抽样误差可以用所有这些可能的实际误差的均方误差表示,也即将抽样误差表示为
̂-θ,所以抽样误差可以用所有这些可能的实际误差的均方误差表示,也即将抽样误差表示为
![]()
其中,MSE  为估计量
为估计量 ̂的均方误差,MSE
̂的均方误差,MSE  的平方根称为估计量
的平方根称为估计量 ̂的标准误。由于θ未知,在通常情况下MSE
̂的标准误。由于θ未知,在通常情况下MSE 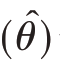 也是未知的。但MSE
也是未知的。但MSE 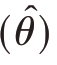 可以分解成:
可以分解成:
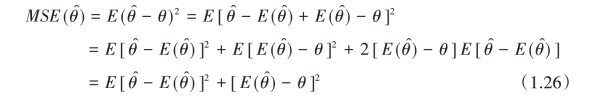
式中第一项是估计量 ̂的方差,记作V
̂的方差,记作V 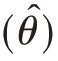 。V
。V  的平方根称为估计量
的平方根称为估计量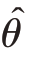 ̂的标准差,记作S
̂的标准差,记作S  。S
。S 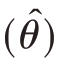 与E
与E  之比称为估计量的变异系数,记为C
之比称为估计量的变异系数,记为C  。式中第二项是估计量
。式中第二项是估计量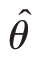 ̂的偏倚B
̂的偏倚B  的平方,即B
的平方,即B 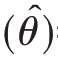 =E
=E  -θ。可以将估计量方差V
-θ。可以将估计量方差V  、偏倚B
、偏倚B  和均方误差的关系用图1-10表示。(https://www.daowen.com)
和均方误差的关系用图1-10表示。(https://www.daowen.com)

图1-10 ![]() 及B
及B![]() 的关系
的关系
一般情况下,均方误差说明了估计量的准确性,而估计量的方差则表明了其估计结果的精确性。通常将精确度定义为估计量方差的倒数,而将准确度定义为估计量均方误差的倒数。
当偏倚B  为零时,称
为零时,称 ̂为θ的无偏估计量,即E
̂为θ的无偏估计量,即E 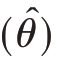 =θ,估计量
=θ,估计量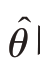 ̂的方差就等于它的均方误差,即
̂的方差就等于它的均方误差,即
![]()
如果 ̂随样本容量n的增大趋近于θ,则称
̂随样本容量n的增大趋近于θ,则称 ̂为θ的一致估计。需要说明的是:①上面所给出的V
̂为θ的一致估计。需要说明的是:①上面所给出的V  的计算公式仍然属于一个理论公式或称为定义公式,在实际中是无法直接应用的。在实际中,计算V
的计算公式仍然属于一个理论公式或称为定义公式,在实际中是无法直接应用的。在实际中,计算V  是依据调查变量的总体方差σ2进行的,当σ2未知时,一般用样本方差s2代替,以对V
是依据调查变量的总体方差σ2进行的,当σ2未知时,一般用样本方差s2代替,以对V  做出估计。②有偏的估计并非都是不可用的,有时有偏估计量在某些方面反而比无偏估计量更好。有研究认为,在实践中当偏倚小于标准误的十分之一时,偏倚对估计量准确度的影响可以忽略不计。
做出估计。②有偏的估计并非都是不可用的,有时有偏估计量在某些方面反而比无偏估计量更好。有研究认为,在实践中当偏倚小于标准误的十分之一时,偏倚对估计量准确度的影响可以忽略不计。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





