如前所述,在容量为N的总体中,抽取容量为n的样本时,可能抽到的样本不止一个。对每一个可能的样本,都可获得统计量样本均值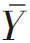 、样本比例p等的一个具体数值。可见,样本统计量是个随机变量。
、样本比例p等的一个具体数值。可见,样本统计量是个随机变量。
我们把根据所有可能样本计算出来的某一统计量的数值分布,称为抽样分布。抽样分布理论是理解抽样调查基本原理的基础。常见的抽样分布有极限分布和精确分布两类。极限分布也称为大样本分布,它只有正态分布一种形式;精确分布又称为小样本分布,其前提是总体服从正态分布,它是正态分布的导出分布,包括有χ2分布、t分布和F分布等形式。
(一)样本统计量的极限分布
样本统计量有很多,这里只考察关于样本均值和样本比例的抽样分布。
例1.1 现从正态分布总体Y~N(100,625)中抽取容量为n=5的所有可能样本,经计算得知样本均值的分布为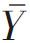 ~N(100,125)。当n=20时,样本均值的分布为
~N(100,125)。当n=20时,样本均值的分布为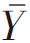 ~N(100,31.25),如图1-5所示。
~N(100,31.25),如图1-5所示。
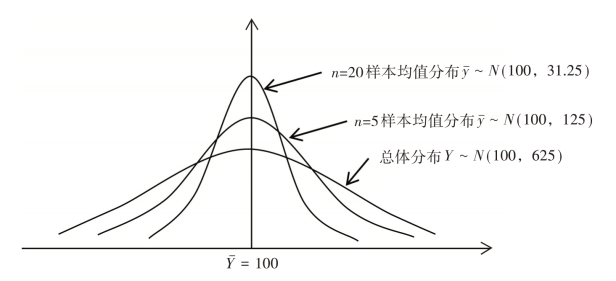
图1-5 样本容量增加后抽样平均数的分布情况
一般地,可以证明如果总体服从正态分布,且总体均值和方差均为已知,即Y~N(μ,σ2),则不论样本量n大小如何,样本均值均围绕总体均值而服从正态分布,并且其抽样分布的方差等于总体方差的1 n,即
n,即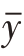 ~N(μ,σ2/n)。
~N(μ,σ2/n)。
而对于非正态总体,若均值μ和σ2有限,则根据中心极限定理,当样本量n充分大时,样本均值仍然围绕着总体均值而近似地服从正态分布,即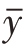 ~N(μ,σ2/n)。
~N(μ,σ2/n)。
例1.2 总体N=5,Y={40,50,60,70,80},则其次数分布如表1-2所示。
表1-2 n=1时样本均值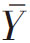 的次数
的次数

E(Y)=μ=60,V(Y)=σ2=200,用图形表示,则如图1-6所示。
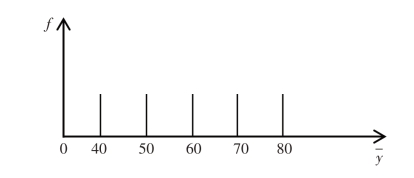
图1-6 n=1时样本均值 的次数分布
的次数分布
若取n=2,用放回抽样则可抽Nn=52=25个简单随机样本,其样本均值如表1-3所示。进一步整理后,即可得出关于样本均值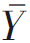 的次数分布情况如表1-4,用图形表示如图1-7。
的次数分布情况如表1-4,用图形表示如图1-7。
表1-3 n=2时样本均值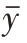
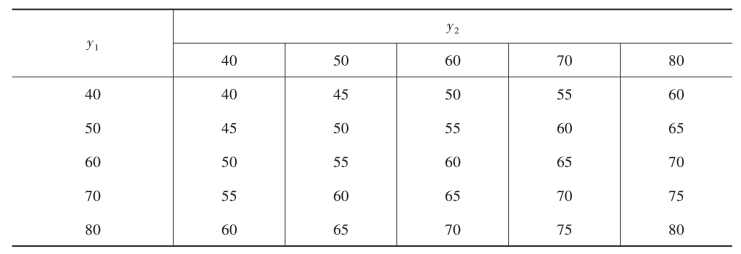
表1-4 n=2时样本均值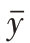 的次数
的次数

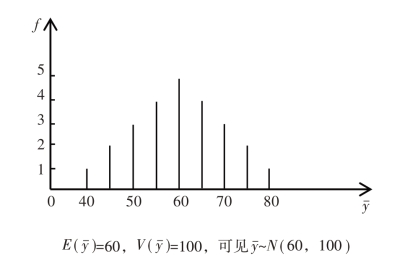
图1-7 n=2时样本均值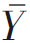 的次数分布
的次数分布
如果总体容量较大,则当样本容量逐步扩大时,样本均值的分布趋于正态分布的趋势更加明显,如图1-8所示。
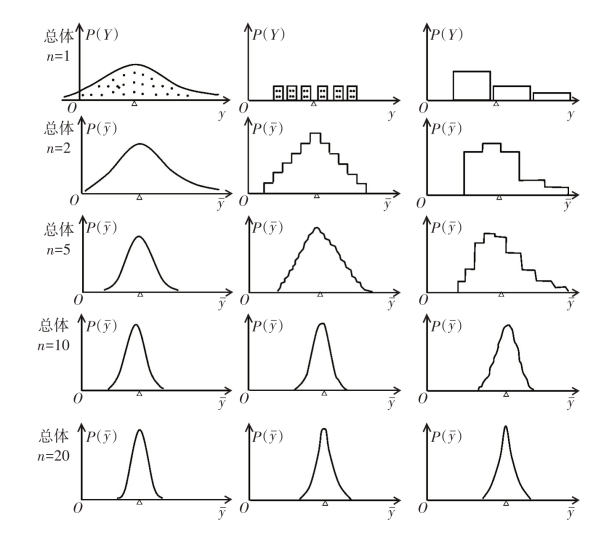
图1-8 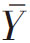 的抽样分布与总体分布的比较
的抽样分布与总体分布的比较
上面的结论在样本比例的抽样分布中同样成立,即对任意一个比例为P的二项分布总体,当n足够大(np>5,n(1-p)>5)时,则样本比例p趋于服从正态分布,样本均值为p,方差为![]() 。因此,标准随机变量
。因此,标准随机变量![]() 趋于服从标准正态分布。
趋于服从标准正态分布。
(二)样本统计量的精确分布
1.χ2分布
设随机变量Yi~N( 0 , 1)(i=1,2,…,n),且相互独立,则Y=![]() 服从自由度为n的χ2分布,记作Y~χ2(n)。(www.daowen.com)
服从自由度为n的χ2分布,记作Y~χ2(n)。(www.daowen.com)
χ2分布的概率密度函数为
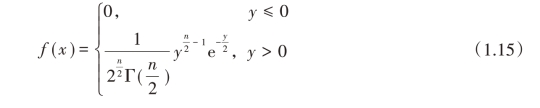
式中,n是正整数,Γ(n/2)是Γ(伽马)函数
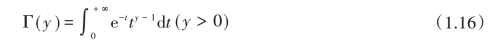
当y=n/2时的函数值。
χ2分布的主要性质有:①f(y)恒为正;②χ2分布呈右偏形态;③χ2分布随n的不断增大而逐渐趋于正态分布。
可以证明,χ2分布χ2(n)的数学期望和方差分别为
![]()
2.t分布
若X~N(0 , 1),Y~χ2(n),且X与Y相互独立,则称随机变量

服从自由度为n的t分布,记作:T~t(n)。
由此也可以推论出关于t分布的如下定义方式:若X~N(μ , σ2),σ2未知,则

服从自由度为n-1的t分布,记作:T~t(n-1),其中: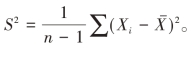
t分布t(n)的概率密度函数为
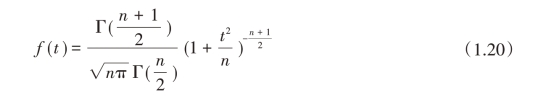
t分布具有如下性质:①t分布对称于纵轴,与N(0 , 1)相似;②在n<30(小样本)时,t分布的方差大于N(0 , 1)的方差;③在n≥30(大样本)时,t分布随n的增大而趋于N(0 , 1)。
可以证明,t分布t(n)的数学期望与方差分别为
![]()
3.F分布
若X~χ2(n1),Y~χ2(n2),且X与Y相互独立,则称随机变量

服从第一自由度为n1,第二自由度为n2的F分布,记作:F~F(n1 , n2)。
如果X~F(n1,n2),则其概率密度函数为
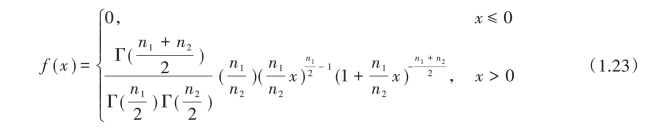
F分布的主要性质有:①F分布呈右偏态;②f(x)恒为正;③在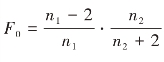 处取最大值(n1>2,f0<1);④随n1,n2的不断增大,F分布的右偏程度逐渐减弱,但不会趋 向 正 态;⑤具 有 倒 数 性 质,即 若X~F(n1 , n2),则1/X~F(n2 , n1);⑥若t~t(n),则t2(n)~F(1 , n)。
处取最大值(n1>2,f0<1);④随n1,n2的不断增大,F分布的右偏程度逐渐减弱,但不会趋 向 正 态;⑤具 有 倒 数 性 质,即 若X~F(n1 , n2),则1/X~F(n2 , n1);⑥若t~t(n),则t2(n)~F(1 , n)。
若X~F(n1 , n2),则其数学期望和方差分别为
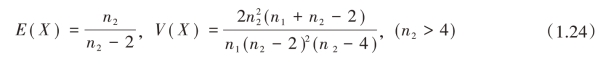
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







