如果总体单元的标志值以总体平均值为中心，形成钟形对称分布，其分布曲线向两侧扩展，逐渐向横轴逼近，无限延伸出去但不接触横轴，则这种分布称为正态分布，或高斯分布、常态分布。服从正态分布的总体称为正态总体。

一个正态分布完全由总体的理论平均值和理论方差这两个参数所决定。如果一个随机变量X服从正态分布，则其分布的密度函数（分布曲线方程，如图1-3）为

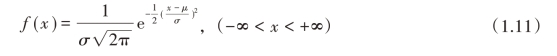
式中，μ和σ2分别为随机变量X的数学期望和方差，π≈3.1416，e为自然对数的底，e≈2.7183。

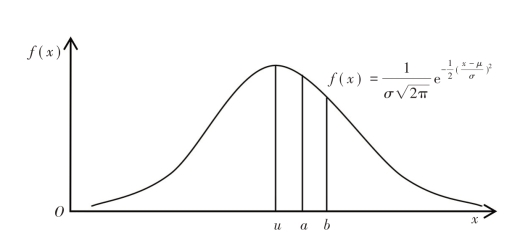
图1-3　正态概率密度曲线

当μ=0，σ2=1时，称该分布为标准正态分布（如图1-4）。

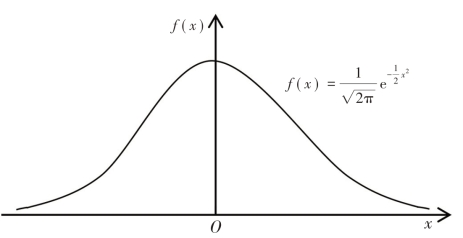
图1-4　正态概率密度曲线

标准正态分布的密度函数为

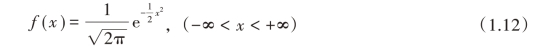(www.daowen.com)

我们知道，全部可能事件发生的概率之和等于1。代表各个体事物分布的正态曲线内面积表明全部可能的事件，因此，分布曲线下x轴以上的面积总保持为1，也即

因此，当σ不相同时，f(x)的形状也不相同，σ越小，分布就越集中在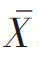附近，σ越大，分布就越平坦。

利用正态曲线的数学性质，依平均值与标准差，可以计算出平均值与某一数值之间的面积，如图1-3中由a到b的面积为

任何正态分布，它的样本落在任意区间（a，b）内的概率等于直线x=a，x=b，横坐标和曲线f(x)所夹的面积（可由正态分布概率积分表查得）。特别地，正态总体的样本落在以下区间的概率为

概率是68.27%；

概率是95%；

概率是95.45%；

概率是99.73%。

正态分布的应用范围很广，是最常见、最重要的分布，居于基础的地位。在生产实践和科学研究中，凡是处于控制状态的数据和测定随机误差的分布，大多是近似地服从正态分布的，所以正态分布的理论对开展社会经济调查和科学研究具有十分重大的意义。