（一）大数定律

大数定律又称平均数定律或大数法则，它所描述的是当样本容量充分大时，样本统计量的极限行为。即在充分大规模的抽样条件下，样本均值和总体均值间的离差可以为任意小这一可能性的概率可以无限接近于1，接近完全的精确性。若从逻辑意义、哲学意义来阐明的话，它是大量现象和过程的规律性，而且一般只有在充分大量观察时，才会显露出现象和过程在某种具体历史环境中具有代表性的主要特征。以下仅对切比雪夫大数定律做一简单介绍。

切比雪夫大数定律：设随机变量Y1，Y2，…，Yn相互独立，且具有相同的数学期望值和方差，E(Yi)=μ，V(Yi)=σ2（i=1，2，…，n），=(Y1+Y2+…+Yn)n，则对于任意正数ε，有

切比雪夫大数定律表明，当n很大时，在概率意义下，随机变量Y1，Y2，…，Yn的算术平均值=(Y1+Y2+…+Yn)/n接近于数学期望E(Yi)=μ，也就是说，在定理条件下，当n无限增加时，n个随机变量的算术平均值将趋近于一个常数。

大数定律表明：

（1）只有掌握足够多的单元数目或样本足够多的情况时，大量现象的规律性及大量过程的倾向性才能很好地显示出来。也就是说，只有在掌握足够多单元数目或样本足够多的情况时，对这些大量现象和过程才能很好地进行研究。

（2）只有在平均数形式上，这些规律性与倾向性才能被表现出来。因此，大数定律又称为平均数定律。

（3）研究大量现象和过程时，如果抽取更多的单位，那么从这些单元的标志值所计算出来的平均值越能够正确地表现出这种现象或过程的规律性。

（4）如果我们研究足够多的单元数目或样本足够多的情况，以平均值为中心，各个单位或情况向正反两方向的离差往往互相均衡化，或者互相抵消。对大量现象或过程来说，这些离差当然不是由于本质的差异所引起，而是由于偶然的状态所发生的。

大数定律的理论和方法，对科学安排统计试验和制定抽样调查方案是十分重要的，它使抽样调查的应用获得充分的数学依据，同时为抽样结果的精确推断提供了充分的可能性。所以说，大数定律是统计抽样调查的数理基础，奠定了用样本估计总体的理论基础，也给统计中的大量观察法提供了理论和数学方面的依据。

因此，在运用抽样调查时，必须注意：①遵循随机原则，只有在随机原则下进行抽样，样本中各单元才能均匀分布在总体中，使样本具有代表性。这样，样本指标才可以用来对总体指标作出估计和推断。②抽样必须注意观察现象的大量性。在同一总体中进行随机抽样，每个被抽中的样本单元的标志值或偏大或偏小，纯属偶然，并不代表总体的数量特征。而通过大量观察，根据大数定律的原理，消除偶然因素的影响，用抽出的单元组成样本综合的结果，才能把总体的数量特征接近准确地反映出来。

（二）中心极限定理(www.daowen.com)

中心极限定理的基本内涵：一组独立同分布变量的平均值，当n充分大时近似地具有正态分布。它分别由德莫佛尔—拉普拉斯和林德伯格—勒维证明。以下仅对德莫佛尔—拉普拉斯中心极限定理做一简单介绍。

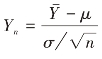设随机变量Y1，Y2，…，Yn相互独立，服从同一分布，且有有限的数学期望值μ和方差σ2，=(Y1+Y2+…+Yn)/n，则　随　机　变　量的分布函数Fn(y)对于任意y，有

通过这个定理，可以知道不论总体服从什么分布，当n 很大时，样本的平均数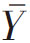近似于具有参数μ和的正态分布（即极限正态分布）。这个定理是大样本统计推断的理论基础。中心极限定理并非证明正态分布的存在，而是用来说明近似地遵从正态分布的概率变量的现象，说明样本平均值的分布接近于正态分布。

中心极限定理表明：样本平均值分布的平均值等于总体平均值，即E(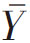)=μ；样本分布的标准差为。中心极限定理奠定了用样本估计量对总体参数进行区间估计的理论基础，利用中心极限定理可以对总体参数做区间估计，并确定其相应的置信概率，是抽样结论可靠性的理论依据。

（三）误差分布理论

抽样调查的目的是把对总体中有限的部分单元的调查结果作为普遍适用于总体的估计和推断。但是，样本是随机抽取的，不同的随机样本就会得出不同的估计量。在同一总体中往往可以抽出多个样本，可以得到同样多的估计量，基于总体指标都存在或大或小或正或负的偏误，因此，用样本指标来推断总体指标，就存在抽样误差。承认这一点，不是证明抽样调查不准确，不能用来推断总体，相反，正是利用可能发生的抽样误差，加上样本指标，来推断在多大的概率度下总体指标在一个怎样的范围之内。

18世纪末，法国数学家拉普拉斯与德国数学家高斯研究误差分布，建立了误差分布理论。

在一个既定的总体中，抽选一定含量的样本，可能抽选到的样本有多个，因此可以取得多个可能的样本指标（主要指均值和比例）。如果将所有可能的样本指标组成频率分布，可发现样本指标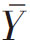越接近总体指标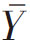的可能样本数越多，即频率越大，偏离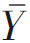越远的可能样本个数越少，即频率越小，形成两端小中间大的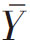可能值的分布，这也就是抽样误差的分布。按正态分布的基本条件，可能样本指标的分布从理论上说是遵循正态分布的。

样本指标的分布，通常又叫抽样分布，数理统计已证明，可能样本指标是否严格遵循正态分布，由两个主要条件所决定：一是抽样总体的分布形态，二是抽样数目的大小。如果样本是抽自正态总体，无论抽样数目是大是小，可能样本指标都是遵循正态分布的；如果样本抽自非正态总体，只要抽样数目较大（n＞30），可能样本指标也是接近或遵循正态分布的。

认识抽样误差及其分布的目的，是希望设计的抽样方案所取得的绝大部分的估计量能较好地集中在总体指标的附近，通过计算抽样误差的界限，使抽样误差处于被控制的状态。