与单参数方法类似，双参数方法也是考察潜在的未观测到的混淆变量对于研究结论的影响。但是，在这个方法中，我们不再将这种影响用一个参数表示，而是用两个参数。仍旧采用上文的表达式，潜在未观测变量u对于个体接受处理变量影响的效果为γ，其他已经观测到的已知混淆变量的影响系数为β，其方程为

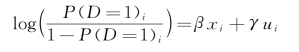
除此之外，我们假设响应变量为Y。Y可以是连续型分布，也可以是离散型分布。以连续型分布为例，假设其呈现正态分布，那么我们可以进一步估算自变量D，观测到的混淆变量X和没有观测到的混淆变量u的影响，假设模型的形式为

其中u服从均值为0、方差为σ2的正态分布。在这个表达式中，在控制了一系列混淆变量X和潜在的混淆变量u以后，D对于Y的效果是τ。基于u对自变量D和响应变量Y的影响，我们可以发现，u的作用是通过γ和δ体现出来的，而敏感性分析所要回答的问题是，γ和δ需要如何变化才能使得τ变得统计上不显著（或者达到某个预定的取值）。为了检验这一点，建立似然函数的对数值。具体而言，基于上述的分布假设，似然函数的对数值可以表达为

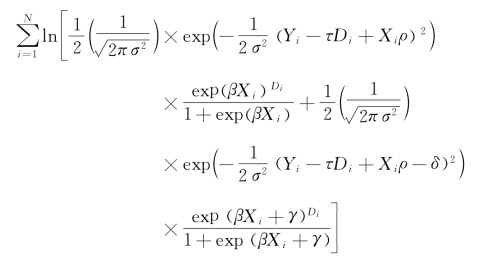(www.daowen.com)

将似然函数的对数值最大化，可以将τ表述成γ和δ的函数。然后看γ和δ如何变化来影响对τ的估计。

目前，双参数方法在STATA中的命令比较简单，使用命令isa自带的数据集，看工会会员对于收入的影响。

图10-3　STATA软件输出结果

在图10-3中，不同的加号的点表示的是测量到的混淆因素对于处理变量与响应变量的联合效果，即每一个的γ和δ的组合。而曲线则是遗漏掉的混淆变量使得一开始估计的因果效果减半的γ和δ的组合。可见，这个混淆变量的γ和δ的组合要比可观测到的混淆变量的γ和δ的组合更加“极端”一些（曲线偏向于右上方）。因此，从这个角度来看，研究结论具有一定的稳健性。