单参数方法的逻辑是这样的。针对一个数据集，每个人进入实验组的概率为P。自然，每个人的p值不同。在前面几章中我们介绍过，用一系列的混淆因素去预测每个人的p值，这就是倾向值。假设这里有两个个体i和j，对于他们，我们有可观测到的混淆变量xi和xj去预测倾向值，但同时，我们怀疑有一些没有观测到的混淆变量ui和uj存在。那么，拟合logistic回归模型，如下所示：

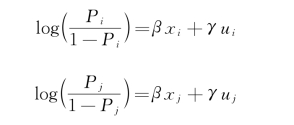
此时，如果我们对比一下个体i和个体j进入实验组的发生比，我们会得到

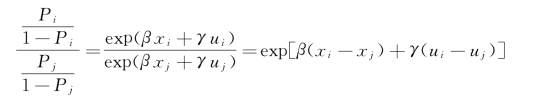
可见，即使我们能够保证这两个个体在可观测到的混淆因素xi和xj上取值完全相等，其倾向值也会因为u上的取值差异而不同。由于传统的倾向值分析方法只是针对x这些可观测变量来计算，我们就可以根据这个未观测到的变量u的取值不同而考察研究结果的敏感性。例如，通过变动u，能得到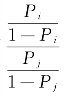的一个可能的变动区间。如果在这个区间内我们一开始的研究结论变化不大，就说明结论具有稳健性，否则就说明有可能受到潜在混淆变量的影响。如果假设u是一个二分变量的话，则我们可以得到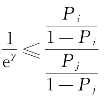≤eγ。进一步，在单参数方法上，如果响应变量Y是一个二分变量的话，可以用Mc Nemar检验。如果响应变量Y是一个连续型变量的话，可以用Wilcoxon Signed Rank Test。

Mc Nemar检验是常用的针对二分变量的检验。例如，处理变量是是否上大学，响应变量为是否为高收入群体。在分析之前，通常会进行匹配，将一些各种背景特征都很相像的两个人进行配对，其中一个没有上大学，一个上了大学。这些配对样本可以放置到一个2×2表格中，假设具体的人数分布如表10-1所示。

表10-1　McNemar检验举例

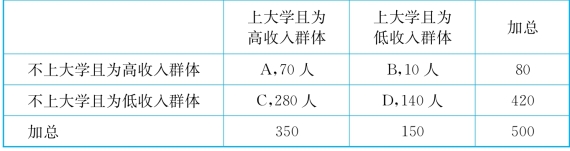
在这些配对对象中，A组上大学和没上大学的人的收入（高收入）一样，D组也是如此，只是都是低收入群体。但是B组和C组不同，在B中，上大学的人为低收入，而不上大学的为高收入。相反，C组的情况正好对调。因为我们关注的是上大学与否对收入的影响，尤其关心上大学是或否能够让人们更有可能进入高收入一组（那么，不上大学的是否更有可能进入低收入一组，即C的情况）。可以说，真正对检验这一因果效果起作用的是B组和C组的人。在零假设下，我们认为上不上大学和收入无关。也就是说，在零假设下，上大学高收入和不上大学低收入，与上大学低收入和不上大学高收入的概率应该都是0.5。换句话说，B组和C组的这290个人，他们进入任何一种情况的可能性都是一样的。此时，可以假设B组和C组联合起来的290个人，每一个人在零假设下服从一个概率为0.5的伯努利分布。那么，290人加起来就是一个二项分布。那么，求p值就是看在这种情况下，出现280个C组人，或者更加极端的情况的概率。所谓更加极端，就是出现281，282，…，直到290个的概率。P的表达式就是

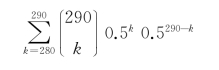
当然，出现观测值或者比观测值更加极端的概率，也可以从B组来进行分析。既然B组的人很少，我们就看达到10人甚至比10人还少的概率，这可以表示为

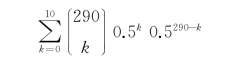
这里，在零假设下，我们认为一个人进入B或者进入C的可能性是一样的，全部都是0.5。但是假设有一些未观测到的混淆因素，会影响大学教育和收入群体的关系。这会影响上面的计算过程。假设我们用q来表示一个人是进入B组还是C组的概率。如上文所述，潜在的混淆因素会影响q，假设混淆因素的影响通过γ来表现出来，如下：

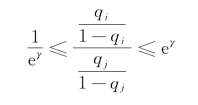
那么，给定一个γ值，一个人究竟属于B或者C的概率可以有一个变动区间，为。那么，在Mc Nemar检验中进行零假设检验的时候，表达式就会有两个端点，分别为

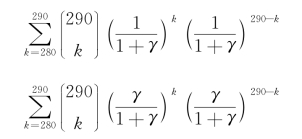
由于我们的计算过程是看出现280个或者更多人进入C组的概率，那么前面一个公式表示当潜在的混淆因素“拉低”进入C组的概率的时候（上大学的人是高收入，不上大学的人是低收入），求得的p值；后者是当潜在的混淆变量“提升”进入C组的概率的时候，求得的p值。从某种意义上说，前面的一个p值是在低估出现我们关心的情形时的p值，而后者是高估出现我们关心的情形的时候的p值。

针对观测到的数据，可以作Mc Nemar检验，如下：

可见，上不上大学和收入的确相关：

(www.daowen.com)

基于这个数据，我们可以进一步通过下面的代码实现敏感性检验：

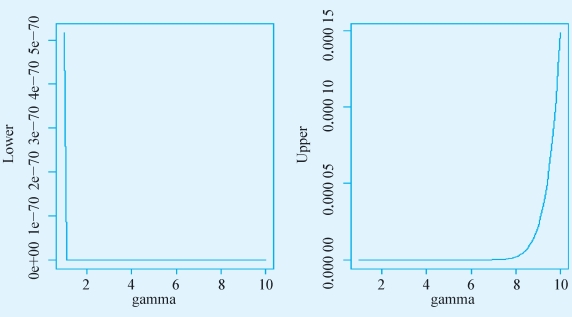
图10-1　R软件输出结果

随着gamma的变化，我们拒绝H0的p值一直在0.001以下，说明我们的结论比较稳健。

对于响应变量为连续型变量的情形，我们可以采用Wilcoxon Signed Rank Test。假设我们同样有一个配对的样本，每一个配对中一个来自实验组，一个来自控制组。Wilcoxon Signed Rank Test检验的思路是，每一个配对中，用实验组个案的Y值减去控制组个案的Y值，将差值的绝对值排序，之后对于实验组Y值大于控制组Y值的那些匹配对的顺序号加总起来，得到统计量T。可以证明，在零假设下，这一加总起来的统计量近似服从正态分布，这个正态分布的均值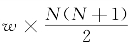为，方差为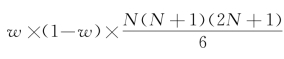，其中，w值为在每一个匹配对下，实验组的个体的Y值大于控制组的个体的Y值的概率。显然，如果处理变量对于响应变量没有影响，w值就是0.5，那么加总起来的顺序号在零假设下服从均值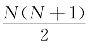为，方差为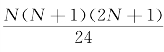的正态分布，因此，我们可以计算统计量的Z值，来进行假设检验。但是，假设有混淆因素影响处理变量和响应变量的关系，这种影响就会干扰w的取值，和上文一样，w在为观测混淆变量的影响下可以有一个区间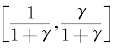，，那么，我们相应的零假设分布就有两种情况，分别为

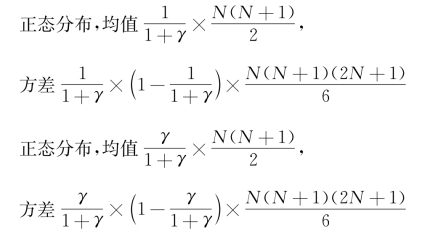
假设我们关心的是情形是相比于控制组，实验组可以提升Y的取值，那么前面一种情况就是在“拉低”实验效果的情况下的零假设分布，后者就是在“提升”处理效应的情况下的零假设分布。上面的分析可以用以下R代码实现：

由于p值在所有的gamma取值下都是小于0.01的，我们可以认为研究结论比较稳健。

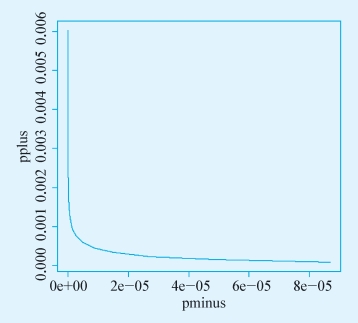
图10-2　R软件输出结果

我们也可以分析一下经典的Lalonde数据中倾向值匹配的敏感性。具体的代码如下：

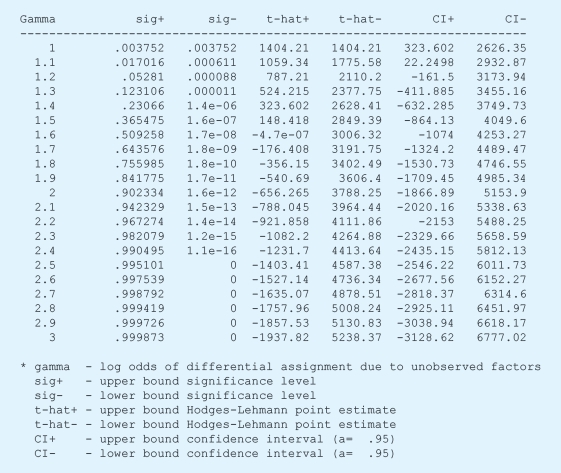
很遗憾，gamma取值只是在1.2的时候，upper bound下的p值就已经大于0.05了。说明结论对于潜在的混淆变量具有比较强的敏感性。在STATA中，我们可以用类似的分析过程，代码和经验结果如下。由于实施结论一致，这里不再赘述。