在连续型处理变量的情况下，基于弱可忽略性假设，我们可以采用广义倾向值调整或者加权的方法来估算因果关系。

表9-7　广义倾向值方法总结（连续型处理变量）

第一个方法可以成为广义倾向值调整。如前所述，所谓调整，就是在估算出广义倾向值之后，将其作为控制变量纳入模型。当然，具体放置的变量形式可以多种多样，例如一次方项、二次方项等。另外一个方法则是广义倾向值加权的方法，即对模型分析的对象进行基于广义倾向值的加权。无论是采用广义倾向值调整，还是广义倾向值加权的方法，我们分析的立足点都在于需要估算出连续型处理变量的广义倾向值。这可以通过以下过程完成：

第一步，基于多个混淆变量，构建模型。在这个模型中，自变量为一系列的混淆变量，响应变量则是连续型的处理变量。最常见的方法是假定连续型处理变量服从正态分布，这样就能够用OLS模型进行估计。

第二步，利用第一步的模型，估算广义倾向值的均值和方差。如果第一步的OLS模型形式为T=Cβ+e（其中T是连续型处理变量，C是一系列的混淆变量，β是其回归系数，e是随机扰动项，且服从均值为0，方差为γ的正态分布），那么，广义倾向值的均值等于Cβ，方差等于γ。

第三步，针对每个被研究对象的连续型处理变量取值，计算其概率。如果是正态分布的话，在连续型处理变量上取值为t的概率p（T=t）等于

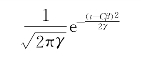
在此广义倾向值的基础上，可以进一步进行回归调整或者加权。在R中，我们可以通过以下代码实现上述分析。假设我们感兴趣的是收入对幸福感的影响。其中收入是一个连续型的处理变量。(www.daowen.com)

相关结果如下所示：

在结束本章之前，我们希望提及的是，如果处理变量是一个连续型变量，那么我们也可以进行广义倾向值的细分（Imai、Van Dyk，2004）。如果处理变量呈现正态分布，甚至都不用估计广义倾向值，这个方法也叫做倾向方程。所谓倾向方程，实际上把这样一个连续性处理变量的分布进一步简化。比如，如果给定X的情况下，处理变量D的条件分布表示为eφ（·|X），其中φ为条件分布的参数。进一步，假设给定X，有一个有限维的参数θ，让eφ（·|X）仅通过θ和X产生联系，那么eφ（·|X）=eφ（·|θ（X））。此时，我们考虑X对D的影响就能够通过直接考虑θ（X）实现。例如，假设在给定X的情况下，D的分布是一个正态分布，它的均值是Xβ，假设它的方差已知，是σ2，这是一个非常常见的假设。这时候的话，D的正态的分布的参数是什么呢？有两个参数，一个是β，一个是σ。这里我们假定σ是给定的，那么参数里面未知的就只是β。这时候的话，β是通过什么样的表达式，能够进入到D的正态分布里面去呢？是Xβ，因为这个正态分布均值是Xβ。至此，我们知道，上面所说的θ（X）就等于Xβ。所有这些分析最后的结论是什么呢？既然给定了X以后，D的分布只能通过Xβ这么一个表达式来展示（即均值）并和一个未知参数产生联系，那我们直接去看这个表达式就行了，因为这个表达式Xβ和eφ（·|X）之间是一一对应了。在特定的情境下，这个分析过程就把问题简化了。知道D的分布，知道其分布的某个参数，通过表达式θ（X）和可观测到的混淆变量X结合起来。这样的话，就不用去看D的分布的具体情况，只需要把关注点放到θ（X）上就可以了。最后做的工作，就变成了：只需要知道这样一个θ（X）和响应变量之间是什么关系，就能估算出来所希望得到的因果效果了。比如，这里θ（X）就是Xβ，就可以把Xβ切成了三段进行细分，每一段估算一下因果效果，然后汇总。

最后我们得到的效果可能如图9-4所示，在θ（X）比较小的时候，它的处理效应比较小，但随着Xβ增加，它的因果效果也在提升。换句话说，处理变量取值变大，处理效应也会大，反之亦然。也就是说，当D从很小的值变到一个很大值的时候，处理效应是在逐渐提升的。

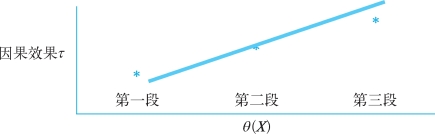
图9-4　倾向方程细分举例