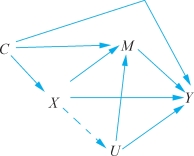
图11-1　因果中介关系图示

如果基于反事实的因果推论框架去考察中介效果，首先要做的是明确进行分析前的基本假设。这些假设可以通过以下的图示方法来讨论。

自变量为X，响应变量为Y，中介变量为M，潜在的发生于自变量之前的混淆因素为C，发生于自变量之后的潜在混淆因素为U。基于这个图示，因果中介分析有四条假设。

①在控制了诸多混淆因素C之后，Y的潜在反事实取值与X独立。这一条件类似于前面章节中谈到的可忽略性假设。由于Y的取值取决于X和M，因此其反事实取值可以表示为Y（X，M）。那么，这条假设可以表示为X⊥Y（X，M）|C。此条假设成立，X的取值分配近似于随机实验，因此就可以估计出X对Y的因果关系。

②在控制了诸多混淆因素C之后，M的潜在反事实取值与X独立。由于M的取值也取决于X，因此M的反事实状态可以表示为M（X）。那么这一条假设表示为X⊥M（X）|C。和第一条假设类似，这一条假设可以保证我们能够估计出X对M的因果效果。

③在控制了诸多混淆因素C和X之后，Y的潜在反事实取值与M独立。此条假设可以表示为M⊥Y（X，M）|C，X。假设②和假设③结合起来也被称为级序可忽略性假设（sequential ignorablility）。基于级序可忽略性假设，我们可以估算出间接因果中介关系，即X如何影响M进而影响Y。

④可能混淆M和Y关系的潜在混淆变量U不能和X有关系。这一条假设的功能在于确保基于上述三条假设估计出的因果中介关系不被发生在自变量之后的潜在混淆变量影响。表示在图中，U和X应当相互独立，即U⊥X。

在满足了上述假设之后，我们便能够进行具体的因果中介效应的估计了。这里，我们有一些术语需要熟悉。如上文所述，响应变量Y的取值取决于自变量和中介变量，而中介变量M的取值取决于自变量。为了表述方便，我们这里依旧假定自变量有两个取值范围，分别标注为0和1。

总效应total effect（TE）=Y（1，M（1））-Y（0，M（0））

所谓总效应，顾名思义，就是指自变量变化带来的Y的变化，其中M因为是自变量X的函数，随X变化而变化。因此当X=1时，M取值为M（X=1），简写成M（1）。同理，对于控制组而言，M的取值是当X=0时的取值，记为M（0）。

自然直接效应natural direct effect（NDE）=Y（1，M（0））-Y（0，M（0））

自然直接效应，是指中介变量取值固定为M（0）时，自变量X变化带来的Y的变化。M（0）的意思是当自变量为0的时候，M的取值。这里，可以发现，Y（1，M（0））是一个“矛盾”的表述，这个表述的意思是，Y的取值是自变量取值为1，但是中介变量取值为M（0）时的取值，因此是一种不能直接观察到的统计量。某个个体的自变量为1时，中介变量应当是M（1），而Y（1，M（0））则要求将中介变量的取值为M（0），故而，这是不能够直接观察到的。

自然间接效应natural indirect effect（NIE）=Y（1，M（1））-Y（1，M（0））

与自然直接效应相对应，自然间接效应将自变量X的取值固定在1，而看中介变量因为自变量从0～1的变化而变化所带来的Y的变化。很显然，对于经验数据而言，我们能够直接看出Y（1，M（1））的取值，但是没有办法直接观测到Y（1，M（0）），即后者也是一种矛盾的状态。

控制直接效应controlled direct effect（CDE）=Y（1，M（a））-Y（0，M（a））

控制直接效应和自然直接效应相比，仍旧是将中介因素的取值固定在某个特定的值上，只是这个值对应于自变量X为a时的取值，而自然直接效应则要求M的取值为X为0的时候的“自然状态”下的取值。控制直接效应的作用在于体现出自变量X和响应变量Y的关系因为中介因素的取值而有所改变的情形。换句话说，在解释Y的时候，如果X和M有交互效应，那么控制直接效应就有用武之地。在此情境下，X对Y的影响取决于M的值。M有几个取值，就有几个X对Y的结果。这实际上是一种直接效应的异质性。当然，如果没有这种交互效应，控制直接效应就等于自然直接效应。除了此种功能之外，控制直接效应还多用于政策研究，即考察当人为干预，设定M为特定取值时，X对Y的效果会如何表现，故而政策分析或者公共卫生领域内较多使用CDE。(www.daowen.com)

纯粹间接效应pure indirect effect（PIE）=Y（0，M（1））-Y（0，M（0））

纯粹间接效应和自然间接效应相比，只是将自变量的取值固定在控制组，而中介变量的取值变化不变，仍旧表示为当D从0到1变化的情况下，M取值的变化。

自然交互效应是指中介效果（间接效应）在实验组与控制组之间有所不同。换句话说，中介效应的大小和自变量的取值之间存在交互关系。在实验组中，中介效应为自然间接效应，在控制组中，中介效应为纯粹间接效应，因此二者的差异代表了自然交互效应。

上述讨论罗列了一系列的统计量以衡量直接效应和间接中介效应。基于这些统计量，我们可以有一系列的总效应分解。

总效应=自然直接效应+自然间接效应

由于自然间接效应可以进一步表示为纯粹间接效应+自然交互效应，因此，我们有

自然间接效应=纯粹间接效应+自然交互效应

将其带入总效应分解公式中，得到：

总效应=自然直接效应+纯粹间接效应+自然交互效应

还可以将自然直接效应与自然交互效应的和定义为总直接效应，即

总直接效应=自然直接效应+自然交互效应

那么，我们对总效应的分解变成了

表11-1　数据可观测性总结

在拿到一个具体的数据后，我们可以按照上面的界定，一一计算出各个统计量的值，以进行相应的效应分解和中介分析。但是问题的关键在于，Y（1，M（0））和Y（0，M（1））并不是直接可测的。我们不得不采用一些统计手段对其取值进行估计。基于自变量和中介变量的取值，我们可以写出不同的组合，如上表所示。对于特定的经验资料，我们可观测到的是对角线上的两个统计量，但是反对角线上的统计量的取值需要想办法间接获得。下面介绍两种方法。