针对多分类的处理变量，广义倾向值分析可以采用四种方法进行，其分别对应于不同的统计假设前提，具体如表9-3所示。

表9-3　广义倾向值方法总结（多分类处理变量）

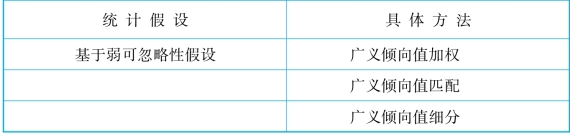
（续表）

如果我们的统计假设前提是弱可忽略性假设，那么我们可以采用传统的匹配、加权或者细分法进行分析。这是因为，在弱可忽略性前提下，我们关注的是特定处理变量水平的效果，这实际上又回到了传统的倾向值分析。例如，假设我们关心不同的教育水平下的收入回报。在分析初中教育的收入回报的时候，在弱可忽略性假设下，看的就是“是否”上初中的收入回报，处理变量又变成了一个二分变量。自然，我们之前使用的各种分析技术也就能用上了。同理，看高中教育的收入回报，处理变量就是“是否”上高中，以此类推。在操作层面上，这将基于对数据的重新编码。还是假设个体有四个教育阶段，那么不同的问题可以有不同的编码方案。

表9-4　编码方案Ⅰ

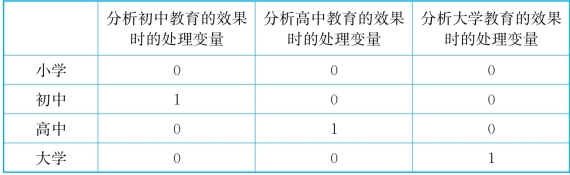
当然，这里看的是特定教育阶段本身的作用，如果看的是特定教育阶段“及以上”的效果的话，编码方式可以是如表9-5。

表9-5　编码方案Ⅱ

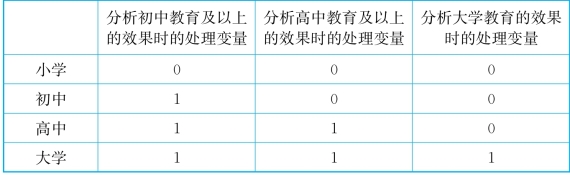
无论采取什么编码方式，我们的处理变量都是一个二分变量。只是对于每一个教育阶段，每个个体有多个处理变量，从而分析出不同教育阶段的因果效果。由于这里的分析过程和前面类似，可以采用前面章节的R代码完成分析。唯一的区别在于处理变量的编码不同。比如，如果我们希望分析初中及以上相对于小学教育水平的因果效果，可以用以下代码完成分析：

加权、细分和匹配的结果分别展示如下：

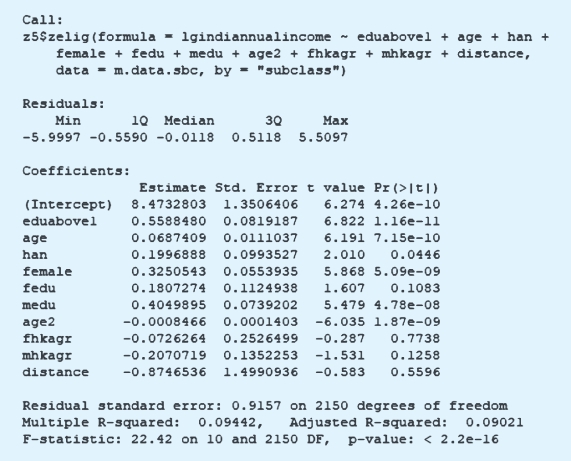
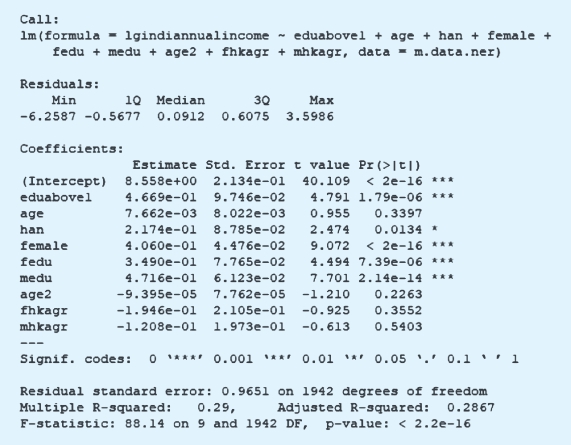
至此，我们知道，基于弱可忽略性假设，研究者可以进行针对两个处理变量水平的比较分析，从而采用传统的倾向值方法进行因果关系的估计。但是，这种分析有自身的局限，即因果效果是不能够“传递”的。所谓不能传递的意思是说，我们可以估计出初中教育相比于小学教育的收入高出a元，高中教育相比于小学教育的收入高出b元，但我们不能够基于a和b的取值进一步推算高中教育相比于初中教育的人的收入高出多少。原因是什么呢？原因就在于，我们基于弱可忽略性假设，每次分析的对象都是对应于整体中的不同部分。

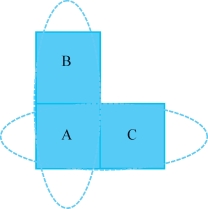
图9-1　传递性举例

比如在图9-1中，A+B是上过小学和上过初中的人构成的匹配对象，A+C是上过小学和上过高中的人构成匹配对象，但如果我们想分析上过高中和上过初中的人之间的收入差异，有可能就要比较B+C构成的群体。既然对于特定的处理变量的水平下，我们所要考察的对象各不相同，当然在下结论的时候就不能通过初中比小学、高中比小学来进一步推断出高中比初中的情况。这就是所谓的缺乏传递性。为了满足传递性，我们需要强可忽略性假设。

需要说明的是，这种传递性的缺乏不会因为基于共同参照对象匹配而完成。也就是说，基于共同参照对象的匹配不一定满足强可忽略性假设。所谓的共同参照对象匹配，是指这样一种思路：假设有三组人，分别设定为T1、T2和T3。我从T1里面选了一个人，然后让他和T2里面的一个人去匹配，同时让他或者她和T3里面的一个人匹配，这时候我就有了一个三人组，通过T1这个人的连接，T2和T3组的人也产生了联系。这有些类似于社会网络分析中的“朋友的朋友还是朋友”这种传递性。但是，即使如此，我们也不能够保证强可忽略性假设。这是因为，虽然我们最后把不同组的对象都放到了一起，我们最多只能够保证三个人中T1和T2的人相像，T1和T3的人相像，而无法保证T2和T3的人相像。换句话说，我们无法保证三个人彼此之间两两相像，因此也就不能够满足强可忽略性假设。这实际上很好理解。假设如下表所示，三个人各有两种颜色作为混淆变量，T1的是红绿，T2的是红黑，T3的是白绿。T1和T2在红色上接近，T1和T3在绿色上接近，但是比较T2和T3，他们之间没有任何颜色相似之处。之所以如此，一个很重要的原因是，我们进行的匹配不可能是精确匹配，因此一些个体之间无法匹配起来的不相似的特征有可能产生这种不传递性。

表9-6　不可传递性举例

那么，如何保证强可忽略性假设成立呢？一个办法是对各个广义倾向值得分进行所谓的广义细分。这里的细分之所以说是广义的，是相对于传统的倾向值细分而言的。由于在二分处理变量的情况下，倾向值p是一个一维变量，因此以前讲的细分可以看成在一条线上进行切割，保证落在某块区域中的个体的倾向值近似。而我们这里说的广义切割，是指在多维情况下的切割，以保证在共同组中的个体在各个倾向值方向上都是近似的。如果处理变量有三个取值水平，那么选取一个作为参照组，另外两个处理水平的广义倾向值构成了一个二维平面，从而可以对平面上的点进行分组，以保证组内的成员在两个广义倾向值维度上都是近似的。同理，如果有四个处理变量取值水平，则三个广义倾向值构成了一个三维空间，我们就可以对处于空间内的点进行聚类，从而保证同类点的广义倾向值近似。具体而言，广义倾向值的广义细分可以用以下代码实现：

不同类别中估计出的因果效果具有比较大的异质性，如图9-2所示。

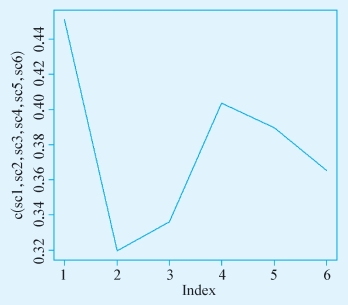
图9-2　R软件输出结果(www.daowen.com)

将这些结果综合起来，我们得到平均因果效果0.397。

在广义细分的基础上，我们还可以进行向量（vector）匹配（Lopez和Gutman，2017）。这个方法可以看作对共同参照对象匹配的一种优化。通过上面对于共同参照对象匹配的描述，我们可以发现，之所以这种匹配过程无法满足强可忽略性假设，是因为两两之间的相像无法保证在其他处理变量水平上的概率（倾向值）相似。比如，我们用一个初中教育阶段的人匹配一个高中教育阶段的人，保证两者进入高中教育（或者初中教育）的概率近似，但是二者有可能在进入大学教育的概率上有很大差异。此时，强可忽略性假设就不能够满足了。因此，为了能够满足强可忽略性假设，需要在进行共同对象匹配时，保证我们关心的两个处理变量水平之外的其他处理变量水平变量上的广义倾向值接近。这就是向量匹配的主要思想。这部分的内容相对而言比较复杂，读者只需了解即可。

具体而言，向量匹配有以下步骤，假设我们的处理变量有四个水平，那么有以下7步。

①利用多分类logistic回归估计广义倾向值，分别表示为p（t=1），p（t=2），p（t=3）和p（t=4）。

②设所有分析对象中p（t=1）的最小值为min（p（t=1）），最大值为max（p（t=1））。同理，计算min（p（t=2））、min（p（t=3））、min（p（t=4））、max（p（t=2））、max（p（t=3））、max（p（t=4））。设置共同取值区间的下限为L，上限为U。则L=max［min（p（t=1）），min（p（t=2）），min（p（t=3）），min（p（t=4））］，U=min［max（p（t=1）），max（p（t=2）），max（p（t=3）），max（p（t=4））］。删除不在共同取值区间内的观测值。

③基于p（t=3），p（t=4）进行K-means聚类（为了扩大取值区间，可以对p（t=3），p（t=4）进行logistic变换），在每个类别内部对T1组的人和T2组的人进行匹配。

④基于p（t=2），p（t=4）进行K-means聚类（为了扩大取值区间，可以对p（t=2），p（t=4）进行logistic变换），在每个类别内部对T1组的人和T3组的人进行匹配。

⑤基于p（t=2），p（t=3）进行K-means聚类（为了扩大取值区间，可以对p（t=2），p（t=3）进行logistic变换），在每个类别内部对T1组的人和T4组的人进行匹配。

⑥将与T1组的人匹配起来的T2、T3和T4组的人合并起来，构成最后的匹配样本。

⑦基于匹配样本，进行因果分析。

我们可以用下面的代码来实现上述分析过程：

经验结果如下：

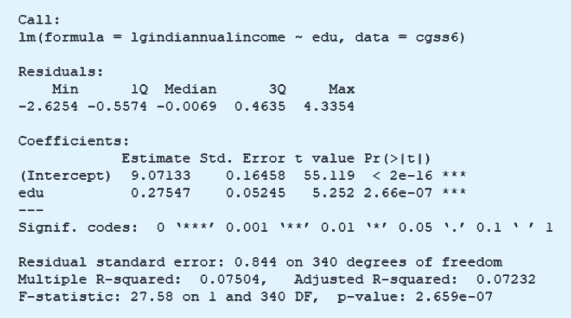
在进入到连续型的处理变量之前，我们有必要介绍一种一般意义上的多类别情境下的匹配。传统的二分类处理变量下的匹配可以称为双边（bipartite）匹配，即从实验组中选取一个或者多个对象和控制组中的一个或者多个对象进行匹配。在多分类处理变量下的匹配则可以称为非双边匹配（non-bipartite matching）。就像上面谈到的，针对每个处理变量的水平，每个人都有一个估计出的倾向值得分。那么，每个人有一个倾向值向量。假设处理变量有四类水平，那么基于特定的参照组，每个人就有三个广义倾向值得分。在非双边匹配下，把每个人和其他所有人的倾向值得分计算距离，比如，我们有三个人的话，就可以两两之间算出三对距离；如果有十个人，十个人里面两两配对，然后算一下倾向值距离。基于这些距离的值，我们进行匹配，当然，匹配的过程有不同的方法，可以用倾向值去匹配，也可以用马哈拉诺比斯距离去匹配。最后我们能够算出一个总体的非双边匹配的距离。既然总体的距离可以表示出来，最后要做的就是最优化的工作。

具体而言，可能一种匹配的方案下得到整体的距离为D1，换一种匹配的方案，又得到D2，换第三种方案又得到D3。很显然，谁和谁配在一起，我们可以不断地调整，直到最后选取整体距离D最小的匹配方案。可以说，非双边匹配是一个非常一般意义上的匹配过程，它的应用范围甚至要比倾向值匹配要广。这里只是举一个很简单的例子，展示一下在R中的操作，这个例子本身也来自R中的nbp Matching程序包。

具体来说，我们模拟两个标准正态分布的变量，分别产生25个观测值。由于只有两个变量，可以用图示的方法展示其分布情况。

采用非双边匹配的话，要求将图中的点进行两两匹配，最后得到下面的结果：

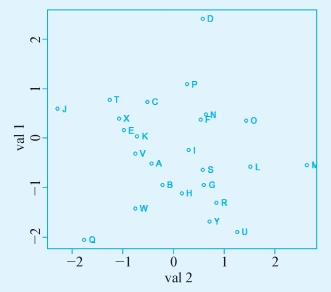
图9-3　R软件输出结果

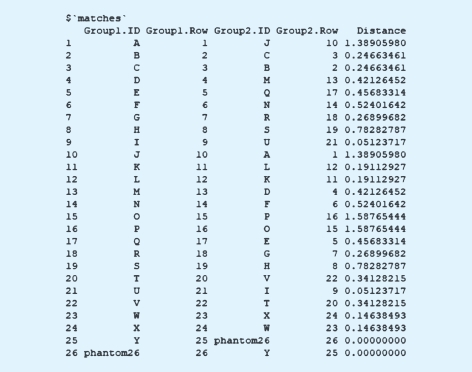
最左边一列可以先不看。后面这一列是第一组（第一个变量）的ID，就是A、B、C、D、E、F、G等。下面一列是行（row）编码。第二组的ID则是Group2.ID这一列。同理，其对应的行数放在了Group2.Row这一列。最后一列是距离。换句话说，如果用A和J匹配的话，那彼此之间的距离是1.38，B和C去匹配的话，彼此之间的距离是0.25，以此类推。但是这里的匹配会有一个问题。即因为最后产生了25个数，是一个奇数，作匹配的话，肯定有一个会落单。此时，电脑会自动产生了一个数，即第26个数，可以称为幻影（phantom）26号。由于是电脑自己补足的一个数字，它自己跟自己匹配，彼此的距离就是0。这就是最后形成的匹配方案。

在STATA中，我们也可以通过加权（例如双重稳健估计）或者回归调整的方法来分析广义倾向值。需要说明的是，所谓的调整，是指在估算出广义倾向值以后，直接将其作为新的控制变量进行处理，其代码如下：

以第一组为参照组，双重稳健估计和回归调整的结果如下：

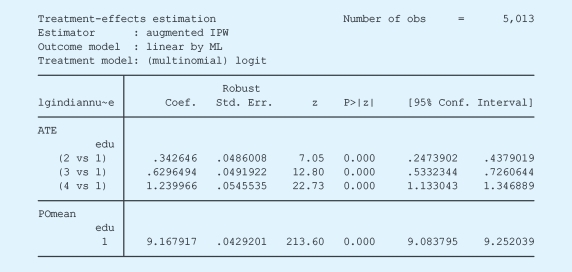
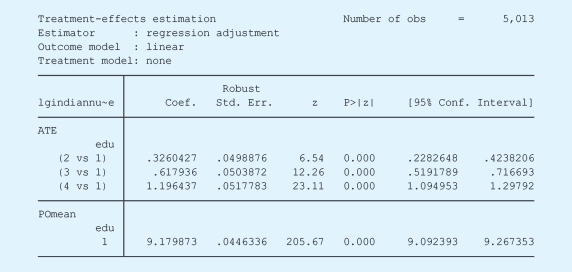
在介绍完多类别处理变量之后，我们下面要讨论的是连续型的处理变量。由于连续型处理变量的类别可以为无穷大，通常难以满足强可忽略性假设。因此，具体的统计分析过程往往关注于连续型的自变量增加或者减少一个单位的情况下，带来的响应变量的取值变化，这近似于在连续型分布上取两点进行比较。鉴于此，我们认为在分析连续型处理变量的因果效果的时候，所基于的假设是弱可忽略性假设。在此假设的基础上，我们可以有两个具体的分析方法（Kluve et al.，2012）。