到目前为止，一般的倾向值都是针对二分处理变量而言的。如果我们用D来表示是否进入实验组（相对于进入控制组而言），那么传统倾向值就是进入实验组的概率，即p（D=1），这就是我们目前为止都很熟悉的通常意义上的倾向值（Feng et al.，2012）。而广义倾向值，则是针对处理变量超过二分型的情形下的倾向值。当然，这里有两种更为具体的情况。第一种情况是多分类的处理变量。比如，传统上可以用上大学与否来衡量一个人的教育水平，这是二分变量。但也可以将个体的教育程度分成不同的类型或者水平（比如小学、初中、高中和大学等，或者同样是上大学，上的什么类型的大学）。这就是多类别处理变量了。第二种情况是连续型的处理变量。比如，我们通常将个体的收入情况（年收入）看作一个连续型的处理变量。那么，如果我们要研究收入对于个体的精神健康状况的影响，处理变量就是连续型的。当然，从数学上来讲，区分连续型变量和离散型变量，看的是我们能否将变量的取值无限细分。离散型变量无法无限细分，但是连续型变量却可以。只是在社会科学研究中，我们不必如此坚持这一数学标准。只要某个变量的取值有很多种情况，且情况与情况之间的状态也有实际差异，那么无论我们是否可以进行无限细分，都可以将其视为连续型变量。通过上面的讨论，可以给广义倾向值一个定义。如果一项研究中的自变量D有很多的层级（可以多到近似于连续型变量的情况），那么个体取特定值的概率就是广义倾向值。可以用以下函数来表示：

广义倾向值=p（D=t），t＞2，乃至是连续型变量

我们知道，为了进行因果推断，需要满足一系列的假设条件。例如，一个假设为正值假设。针对二分变量时，正值假设是说，一个人进入实验组还是进入控制组均有可能，其进入实验组或者控制组的概率是在0～1的一个值，但是不能取值为0或者1。这个假设如果把它扩展到广义倾向值的情景下，就意味着每个人接受处理变量每个水平的概率都要在0～1。换句话说，如果我们分析的是小学、初中、高中、大学这四个教育等级的某种影响的话，那么正值假设就要求每个被研究对象进入到每一个特定教育等级的概率都是0～1的一个数。也就是说，每个人都有可能是小学毕业，也有可能是初中毕业，也有可能是高中毕业，也可能是大学毕业。可见，在广义倾向值的分析问题中，正值假设要比之前的正值假设要复杂。如果我们只是看是不是上大学，那么我们只要求每个人都有“可能”上大学，因为不上大学是上大学的一个很直接的反面状态，如果每个人都有可能上大学，就相当于说每个人都有可能不上大学。但是如果我们的处理变量有很多类别的话，那么针对每一种情况，我们要求每个人都有可能处于此种状态，自然是一个更严苛的标准了。

除了正值假设之外，我们在做因果推断的时候，还需要满足的是可忽略性假设，即在控制了一系列控制变量X或者由其生成的倾向值得分之后，处理变量和响应变量各个潜在取值之间保持独立。在广义倾向值中，可忽略性假设有两种类型。一种是非常强的可忽略性假设，指当我们控制了很多控制变量X之后，或者控制了一系列的广义倾向值得分p（D=1），p（D=2），…，p（D=t-1）以后，处理变量D和各种各样的潜在的Y（t）都是独立的，如下所示：

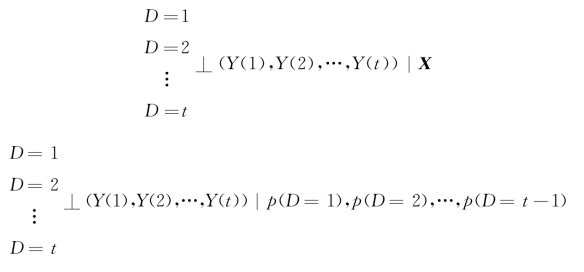
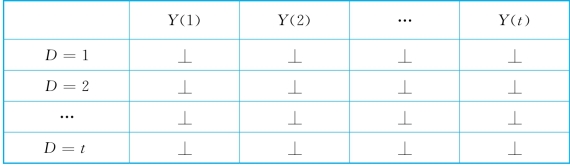
为了理解这一假设的独特性，将其与传统的可忽略性假设进行对比。对于二分型处理变量而言，要求D的取值（0或者1）与Y（1）和Y（0）彼此之间是独立的。但是在强可忽略性假设下，要求D和多个潜在响应变量Y（1），Y（2），…，Y（t）彼此独立。举了例子来讲，一个人是不是高中毕业和他如果是小学毕业的情况下的收入是独立的，一个人是不是大学毕业和他如果初中毕业的话的收入情况彼此之间是独立的。这构成了一个独立性矩阵如表9-1。

表9-1　强可忽略性假设

(www.daowen.com)

与强可忽略性假设相对应，一个弱的可忽略性假设不再坚持这样一个矩阵式的独立性要求，而只是要求当处理变量处于特定取值水平下，处理变量的取值和响应变量在那一特定取值水平上的潜在结果彼此独立。例如，基于特定的参照组（小学教育水平），我们想看初中教育相比于小学教育对收入的影响，只需要保证在控制了个体（相比于小学阶段的教育）进入初中教育阶段教育的概率的前提下，个体是否取得初中教育文凭与个体在小学教育水平或者初中教育水平下的潜在收入情况彼此独立，即

如果我们用矩阵的形式来表示弱可忽略性假设，如表9-2所示。

表9-2　弱可忽略性假设

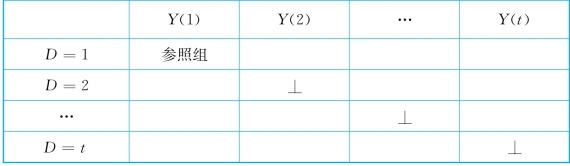
通过对比强可忽略性假设与弱可忽略性假设的这两个矩阵，我们不难理解为什么后者称为弱假设。这里只要求在对角线上满足可忽略性假设，而非对角线则不在考虑之列。也就是说，弱可忽略性假设是针对特定的处理变量水平而言，而强可忽略性假设则不限于特定的处理变量水平，属于一种普遍意义上的可忽略性。

在介绍完广义倾向值的基本前提假设之后，下面的分析将基于处理变量的特征（多分类还是连续型处理变量）分别进行讨论。