目前为止，我们介绍了工具变量的基本特征以及实际操作。特别强调的是，工具变量可以帮助研究者处理“样本不服从”问题，因此在很多具体的实践中，有很广泛的应用范围。下面我们要介绍的是，在利用工具变量进行因果推断的时候需要满足哪些基本条件。正如本书一开始所谈到的，进行因果推断的时候，如果前提假设条件不成立的话，即使采用了工具变量的方法做因果推断，得到的结论也会受到质疑。

在讲基本假设之前，不妨先介绍一个非常经典的工具变量。按照Thad Dunning的总结（Dunning，2012），目前在社会科学研究中，最好的一个工具变量就是美国的通过抽签上战场这个工具变量。因为它基本上满足了几乎所有的因果推论需要满足的条件。具体而言，如果我们想知道战场经历如何影响了后续的劳动力市场表现。很显然，我们不可能直接安排个人上战场。但是当时美国的安排是抽签决定，假设号码从1～6，抽中1、2、3则上战场，抽中4、5、6则不需要上战场。如果我们套用一下上面的讨论，工具变量是抽签的结果，号码是大还是小完全是自己随机抽取的，就像随机实验一样。但是我们关心的不是抽中号码的大小，而是关心是不是真的上战场，后者就是我们的处理变量。而响应变量则是一些劳动力市场上的表现，比如退伍以后进入劳动力市场的话收入是多少。基于这样一个经典的例子，我们来具体看一看，如果基于工具变量来进行因果推断的话，需要满足什么条件。具体而言，有五条条件需要满足（Angrist，Imbens和Rubin，1996）。

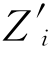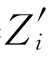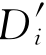第一条条件就是我们以前谈到的SUTVA。在本书开始的时候，我们讲过，SUTVA有两层意思，一个是处理变量不存在版本差异，另一个意思是个体的Y的取值不受其他个体的处理变量安排方式的影响。在工具变量的方法体系中，SUTVA可以表述为两点：（1）如果Zi=，则Di（Z）=Di（Z′）；（2）如果Zi=，Di=，则Yi（Z，D）=Di（Z′，D′）。

其中，向量Z是一个群体中的号码分配方式，例如一群人有5个人，最后的号码抽取方案为1、2、2、1、5、6。则Z=（1 2 2 1 5 6），D=（1 1 1 1 0 0）。条件（1）是说，对于编号为三的个体而言，他肯定要去上战场，而这个决定与其他人抽签结果无关。也就是说，只要第三个人的抽签号是2，那么换一种其他人的抽签情况，不改变第三个人是否上战场D3的取值。例如，再抽签一次，得到的Z′=（5 5 2 2 3 6），D′=（0 0 1 1 1 0）。也就是说，编号为1号，2号的人将从上战场改为不上战场，而5号则由不上战场改为上战场，但这些都不影响3号的D3的取值。同样的道理，响应变量潜在的取值Y也不会随着其他人的抽签结果和是否上战场而改变。这是SUTVA的条件2所讲到的内容。除了不存在相互影响之外，这里的表述也说明不存在版本的差异。例如，当Z固定下来以后，D的取值是唯一的，Z不存在同样取值但是D的版本有差异的问题（例如同样是抽中1，一些人上战场，而一些人不去，这是不行的）。同理，只要Z和D定下来了，Y的潜在取值也就定下来了。实际上，根据一致性的假设，Z和D定下来之后，Y的潜在取值就是Y的观测值了。

第二个条件是随机化假设，即Z是一个随机化过程得来的工具变量。表述为Z为特定取值c的概率等于Z为特定取值c′的概率。这怎么理解呢？假设我们有三个人，每个人抽取号码，每个人有六种可能取值，则三个人综合起来有63=216种取值组合，每一种组合都是等可能性的。换句话说，由于是随机实验，因此在这216种组合中，实际出现的某种组合的概率都是1／216。

第三个条件是排除性假设（exclusion）。这个假设的意思是Z对Y的影响只有通过D的传递才能发生。Z和Y之间不存在直接的联系，表述如下：

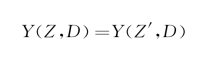
这个表述所要传达的意思是，既然Z对Y的影响通过D完成，那么只要D定了下来，Y就不可能再受Z的影响了。即使我们把Z的安排改变成Z′，但是只要D不变，Y也不变。

第四个条件很简单，即要求Z对D具有实质性的影响。放在上面的例子中，这一条假设要求抽签的结果Z和是否上战场D之间应该是相关的。二者的相关性不能是0。

第五个条件是单调性假设（monotonicity）。意思是说，当Z变化，D的变化服从一定的单调性。比如，如果Z从小号码到大号码变化的话，D的变化方向应当是从不上战场的概率大到上战场的概率大。二者之间的变动方向应该是一致的。这一个假设之所以重要，是因为它可以帮助研究者把一类人排除出了我们分析之外，哪一类人呢？就是唱反调的人（defier）。所谓唱反调的人，是指当他抽中的号码是大号的时候，本来不用上战场，但他反而坚持一定要去。或者如果他抽中号码是小号，本来需要去前线，结果他由于各种原因没有去前线。为什么我们一定要把这些唱反调的人排除出去呢？这可以从我们计算因果效果的公式看出来。正如上文所示，利用工具变量进行因果推断，所依据的统计量是Z与Y的协方差比上Z与D的协方差。但是，基于Z带来的D的变化有两种情况，一个是当Z逐渐变大的时候，D逐渐变小（负相关），或者Z逐渐变大的时候，D逐渐变大（正相关）。对于我们的研究而言，Z的效果需要保证Z和D的共变能够反映出理论上有意义的问题，即当号码从小号转为大号的时候，人们上前线的概率下降。假设取的号码是小号的话Z=1，取大号的话Z取值为0。D的编码为D=1上前线，D=0不上前线。那么单调性假设要求D（Z=1）≥D（Z=0）。这样，那些唱反调的人（对于他们，D（Z=1）＜D（Z=0））就被排除出去了。

这五个条件综合起来，就能够帮助我们基于工具变量方法进行因果推断。例如，有了SUTVA和随机化条件，Z的实施是一个随机实验，那么我们就能够计算出意向处理效用。条件三和条件四加起来就是工具变量的定义，条件五帮助去掉了唱反调的人。由此，我们能够估计出因果效果。

但是这里需要说明的是，通过工具变量估算出来的因果效果是针对特定人群的，这些特定人群是那些服从研究者设计的对象。因此，通过工具变量估计出来的因果效应也称为局部处理效应（local average treatment effect）。如果以上面谈到的验证药效的例子来说明，所谓的吃药后的效果仅仅是限定在那些实验组中实际吃药，而控制组中不吃药的那些听话的人而言的。广义上看，任何一个实验中，分析对象群体都能分为四种人，一种是这里所谓的听话的人，一种是无论研究者如何安排总是吃药的人，一种是无论研究者怎么安排都不会吃药的人，而最后一种就是我们上面说的唱反调的人。我们通过工具变量所估计出的因果效果仅适用于那些听话的人。唱反调的人基于上面的单调性假设已经排除在外。总是吃药或者总是不吃药的人，它们的处理变量是一个常量（D总是为0后者1），自然无从分析其处理效应。

为了更好地理解局部处理效应，我们可以采用图示法来表示不同类型的对象。对于听话的个体而言，工具变量可以影响处理变量，从而进一步影响Y。由于听话的个体其处理变量的取值取决于工具变量的取值，因此混淆变量U不会影响自变量D（见图6-2）。

但是对于那些总是吃药或者总是不吃药的人而言，处理变量的取值和工具变量没有任何关系，由于二者之间不存在任何联系，我们自然无法估计因果效果（见图6-3）。

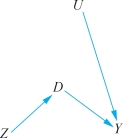
图6-2　听话者示例(www.daowen.com)

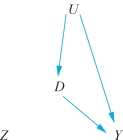
图6-3　总是接受特定处理变量水平影响的个案示例

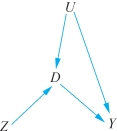
图6-4　去除不听话的个案后的样本示例

基于单调性假设，我们把唱反调的人排除出去的话，所处理的对象相当于把这两张图重叠起来，得到图6-4，这实际上就是本章一开始时所展示的工具变量的图示。

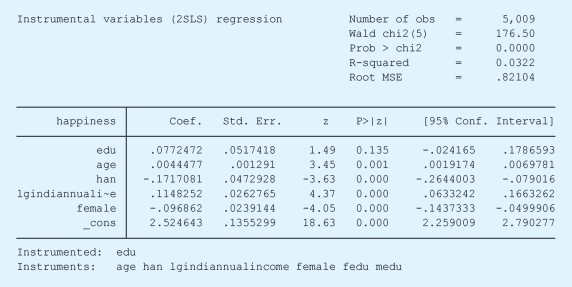
工具变量的方法软件实现时非常容易。假设我们以父母的教育水平作为工具变量，看个体的教育水平与幸福感之间的关系，那么R里面的代码如下：

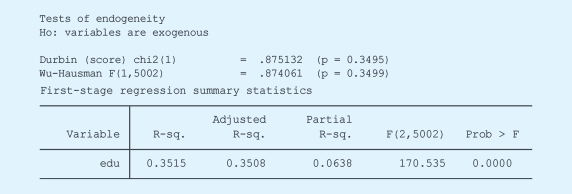
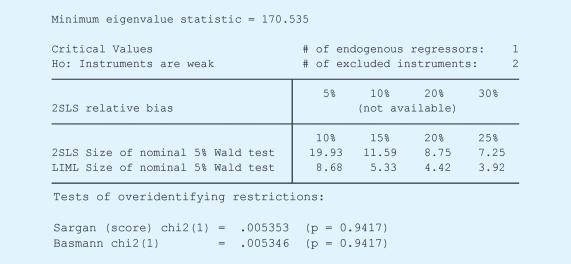
相关分析结果的解释与常规的回归模型一样，这里不再赘述。只是需要说明的是，在分析结果之后，有几个指标衡量了工具变量的优度。其中弱工具变量指的是当我们用工具变量去预测自变量取值的时候，模型的解释力很差。通常在线性模型中，我们可以用F检验中的F值来衡量工具变量（和其他控制变量一起）对于处理变量的解释力。Wu-Hausman检验看的是不用工具变量的OLS模型与采用工具变量的OLS模型进行对比的时候，结论是否一致，如果一致的话，就说明内生性问题不是很严重，不必要使用工具变量。Sargan检验是针对多个工具变量的情况所做的检验，如果原假设被拒，则说明至少有一个工具变量不合适。

在STATA中，工具变量的分析代码如下：

相关的经验发现与上面的一致，这里不再赘述。