加权的意思是指可以把倾向值作为基本的构建权重的变量。回想前面章节中关于加权的基本思路，可以发现，倾向值因为衡量了一个个体进入实验组的概率，那么它的倒数就可以作为权重来对实验组中的个体使用，从而估计出“如果”所有人都进入实验组的话，他们响应变量取值的期望值是多少，亦即E［Y（1）］。同理，对于控制组中的人而言，他们的权重就是1减去倾向值。基于此进行加权，我们就能够知道“如果”所有人进入实验组的话，在响应变量上的取值的期望值，亦即E［Y（0）］。具体而言，我们有：

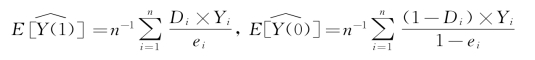
此时，我们关心的因果效果（如果用τ表示）就是

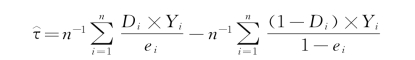
这里需要提到的是，倾向值加权的方法还可以和传统的回归方法结合起来，从而构成我们所谓的双重稳健估计法。为了更好地理解双重稳健估计，我们暂时假设，有一个很好的模型可以刻画响应变量、自变量和混淆变量之间的关系。例如，对于连续型自变量Y，可以假设以下模型（其中混淆变量矩阵表示为X）。

对于二分型响应变量，我们可以假设传统的logistic回归模型，即

对于连续型的Y而言，

而对于二分型的Y而言，我们有

但是，这样一个完美的模型很难估计得出。原因很简单，任何线性模型的形式都是基于研究者的假定。我们无法完全了解是否这一模型对于现有数据就是“对”的。例如，我们在拟合模型的时候不知道是否已经纳入需要的所有的控制变量，无法得知自变量的测量是否存在误差，更无法验证我们设定的线性模型形式是否恰当。因此，如果模型设置有误，我们就不能够将回归模型的特定系数看成对因果关系的一个无偏估计。那么，我们有没有可能将倾向值加权的方法与回归方法结合呢？答案是肯定的。这就是所谓的双重稳健估计方法。具体而言，对于因果关系的双重稳健估计量可以表示为

实际上，双重稳健估计可以看作对倾向值加权方法的一个调整。具体而言，通过简单的数学变换，可以将其表示为

前面一行的表达式就是传统的倾向值加权下对因果关系的估计，后面的是调整部分。Glynn和Quinn（2010）证明，后面的调整部分的期望值为0。

综上，双重稳健估计之所以如此命名，是因为只有在回归模型与倾向值模型都出问题的情况下，其对因果关系的估计才会有所偏差。这相比于单纯使用回归模型或者单纯使用倾向值模型更加“保险”。因此，经验研究者如没有很强的证据表明（1）回归模型设定是正确的或者（2）所有的混淆变量均已经考虑到。那么，双重稳健估计方法不失为一个很好的选择。在计算得到了双重稳健估计量以后，其统计估计的标准误可以通过自助法算得，这里不再赘述。在R中，双重稳健估计可以通过以下代码实现，还是以Lalonde的数据为例：

(www.daowen.com)

可以发现，双重稳健估计的因果效果与单纯利用倾向值加权和单纯利用回归模型的结果还是有些不同的。

在STATA中，我们也可以进行倾向值加权和双重稳健估计，代码如下：

基于倾向值加权，如果所有人的treat变量的取值都是0，则其收入情况为4 563.123，但是如果所有人的treat变量都取值为1，则平均收入要比4 563.123高1 625.424元。

基于双重稳健估计，如果所有人的treat变量的取值都是0，则其收入情况为4 592.75，但是如果所有人的treat变量都取值为1，则平均收入要比4 592.75高1 700.768元。

在这个命令之后可以使用其他补充命令，检测混淆变量的平衡性以及在加权以后实验组与控制组在接受处理变量影响的概率上的重叠性（overlap）。

图5-2　STATA软件输出结果

以年龄变量为例，可以发现在加权前后，平衡性有一个很好的改善。

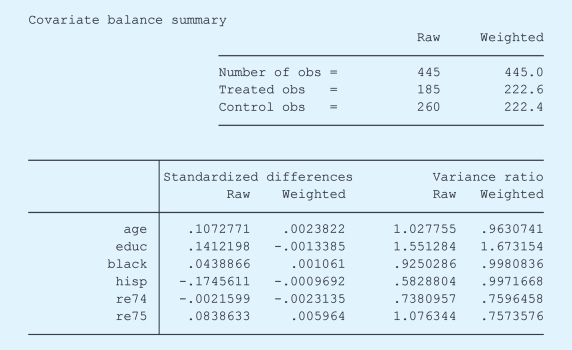
整体而言，所有的混淆变量都能够满足平衡性。

图5-3　STATA软件输出结果

最后，可以发现，实验组与控制组之间的倾向值重叠度也比较高。