4．1．2．1　分析师行为价值函数下的静态博弈

考虑一个完全完美信息静态博弈，该博弈中明星分析师与一般分析师同时行动，其效用水平由式（4-2）、式（4-3）决定。模型基本设定如下。

（1）局中人。

明星分析师与一般分析师。

（2）局中人策略。

分析师决策是否发布标新立异的观点。

（3）局中人效用。

明星分析师发布标新立异观点获得的效用为Ustar1＝Ustar（special＝1，...），发布跟风观点获得的效用为Ustar0＝Ustar（special＝0，...）；一般分析师发布标新立异观点获得的效用为Uother1＝Uother（special＝1，...），发布跟风观点将获得Uother0＝Uother（special＝0，...）。在控制其他变量不变的情况下，有Ustar1＞Uother0＞Uother1＞Ustar0，即明星分析师通过发布标新立异的观点获得更高的满足感，明星分析师对发表跟风观点表现出显著的厌恶，一般分析师通过发布跟风观点（即重复市场上既有研究报告的研究结论）达到规避风险的目的，以获得相对更高的效用水平。对应的收益矩阵如图4-1所示。

图4-1　分析师行为价值函数下的静态博弈收益矩阵

（4）纳什均衡及解释。

通过重复剔除严格劣势策略(strictly dominated strategy)，可知模型唯一的纳什均衡为（special＝1，special＝0），相应的效用为（Ustar1，Uother0），即明星分析师选择发布标新立异的观点，一般分析师选择发布跟风的观点。

4．1．2．2　分析师依次决策下的序贯博弈

为了刻画分析师发布研究报告的先后顺序差异，考虑一个明星分析师与一般分析师先后作出估值决策的序贯博弈，该博弈中明星分析师先作出对公司股票价格的判断，一般分析师在观测到明星分析师估值判断后再出具估值预测。模型基本设定如下。

（1）局中人。

明星分析师与一般分析师。

（2）局中人策略。

明星分析师与一般分析师依次发布对公司价值的判断，分别为Pstar和Pother。

（3）局中人效用。

明星分析师将最小化股票市场价格预期与公司内在价值期望间的误差，即明星分析师的效用函数为Ustar＝U1－（E（P）－E（P*））2，其中，E（P）为市场价格预期，在市场中存在测度分别为p和1－p的明星分析师和一般分析师的情况下，E（P）＝p*Pstar＋（1－p）*Pother；一般分析师将最小化自身估值预测与其可观测到的明星分析师估值预测间的差距，即一般分析师的效用函数为Uother＝U2－（Pother）2，其中＝Pstar＋ε，ε表示市场信息传递噪音，满足ε≠0。

整个序贯博弈的过程如下。

阶段1：明星分析师发布预测Pstar。

阶段2：一般分析师观测到有噪音的明星分析师预测结果在此基础上给出自己的预测Pother。至此，市场价格预期形成，一般分析师与明星分析师的效用实现。

（4）均衡求解。

采用逆向归纳法求解该博弈均衡。

阶段2：一般分析师在观测到有噪音的明星分析师预测结果时，由于不知道噪音的方向和大小，因此，为了最大化Uother＝U2－选择发布的预测结果＝Pstar＋ε，即一般分析师将完全按照其可观测到的明星分析师的有偏预测结果发布估值，在均衡时获得收益为

阶段1：给定一般分析师将以＋ε发布估值预测，明星分析师将最大化Ustar＝U1－［E（P）－E（P*）］2＝U1－［p×Pstar＋（1－p）－E（P*）］2，即最小化［p×Pstar＋（1－p）×（Pstar＋ε）－E（P*）］2＝［Pstar＋（1－p）×ε－E（P*）］2，则有明星分析师在均衡时的估值预测为）－（1－p）×ε，在均衡时获得收益为

（5）均衡及解释。

通过逆向归纳法求解，可知该模型的均衡为［E（P*）－（1－p）×ε，E（P*）＋p×ε］，相应的效用为（U1，U2），即明星分析师发布的估值预测为＝E（P*）－（1－p）×ε，一般分析师发布的估值预测为＝E（P*）＋p×ε。该均衡结果表明，如果明星分析师对市场噪音误差能够有较为准确的估计，其能够通过自身估值策略的调整使得市场价格预期在均衡时处于相对台理的位置。

4．1．2．3　分析师类型未知下的信号博弈

考虑一个市场中存在明星分析师和一般分析师但投资者由于信息缺失而不知道其类型的信号博弈模型，投资者通过观测分析师的行为特征判断该分析师类型并作出相应决策。模型基本设定如下。

（1）局中人。

同质的投资者和异质的分析师，分析师分为明星分析师和一般分析师两类，分析师是明星分析师的先验概率为0.2，分析师是一般分析师的先验概率为0.8^[1]。

（2）局中人策略。

分析师决策是否发布具有标新立异观点的报告，标新立异观点正确的概率为α，错判的概率为1－α（满足α＞1/2）。投资者根据分析师发布的报告来决定自己是否采纳观点。(www.daowen.com)

（3）局中人效用。

对明星分析师来说，如果其标新立异的报告被采纳，可获得Ua单位的效用；如果其报告不被认可，则获得Ub单位的效用。当明星分析师发布跟风观点时，被采纳和不被采纳时的效用分别为Uc、Ud。对一般分析师来说，如果其标新立异的报告被采纳，可获得Uc单位的效用；如果其报告不被认可，则获得Ud单位的效用。当一般分析师发布跟风观点时，被采纳和不被采纳时的效用分别为Ua、Ub。效用大小满足Ua＞Ub＞Uc＞Ud（相对于观点不被采纳，观点被采纳能够获得更高的效用；发表标新立异观点对一般分析师来说需要消耗更多精力，获得的效用相对更低）。对投资者来说，其采纳的证券分析师报告为标新立异观点时，如果与市场真实情况相同，则获得Ue单位的效用，如果与市场真实情况不符，则获得零单位的效用；其采纳的证券分析师报告为跟风观点时，如果与市场真实情况相同，则获得Uf单位的效用，如果与市场真实情况不符，则获得零单位的效用。

整个博弈的过程如下。

步骤1：证券分析师选择是否发布标新立异观点的报告。

步骤2：投资者根据自己对分析师类型的信念，选定自己是否采纳分析师的报告。

步骤3：证券分析师和投资者的期望效用实现。

（4）均衡求解。

上述博弈过程可用图4-2表示。其中，分析师具有两种类型：t1表示明星分析师，t2表示一般分析师。

对上述信号博弈，可能存在混同纯策略纳什均衡或（和）分离纯策略纳什均衡。

①混同纯策略纳什均衡。

若明星分析师与一般分析师在均衡时的策略分别为（发表标新立异的观点，发表标新立异的观点），则投资者无法判断分析师的类型，其认为分析师是明星分析师的概率为0.2，分析师是一般分析师的概率为0.8。在此情况下，投资者选择采纳分析师标新立异的观点的期望收益：

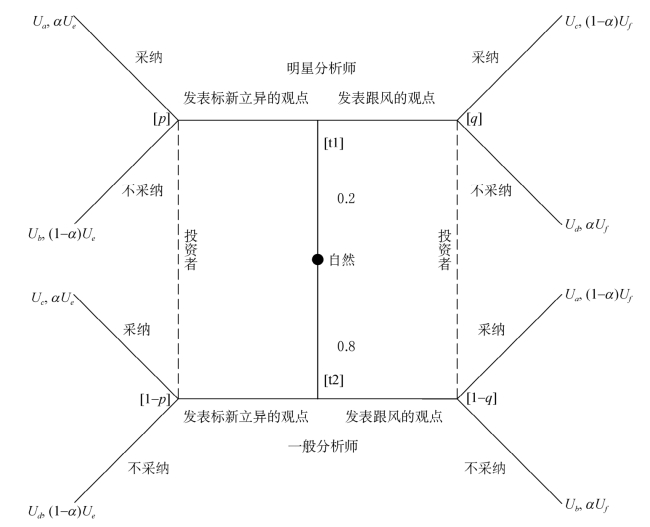
图4-2　信号博弈示意图

E1＝0.2×αUe＋0.8×αUe＝αUe

投资者选择不采纳分析师标新立异的观点的期望收益：

E2＝0.2×（1－α）Ue＋0.8×（1－α）Ue＝（1－α）Ue

当α＞时，E1＞E2，投资者选择采纳分析师标新立异的观点。

在给定投资者选择采纳分析师标新立异的观点的情况下，一般分析师会选择偏离均衡（因为无论投资者在观测到跟风的观点时选择何种策略，一般分析师均会获得更高的收益）。

若明星分析师与一般分析师在均衡时的策略分别为（发表跟风的观点，发表跟风的观点），则投资者无法判断分析师的类型，其认为分析师是明星分析师的概率为0.2，是一般分析师的概率为0.8。在此情况下，投资者选择采纳分析师跟风的观点的期望收益：

E1＝0.2×（1－α）Uf＋0.8×（1－α）Uf＝（1－α）Uf

投资者选择不采纳分析师跟风的观点的期望收益：

E2＝0.2×αUf＋0.8×αUf＝αUf

当α＞时，E1＜E2，投资者选择不采纳分析师跟风的观点。

在给定投资者选择不采纳分析师跟风的观点的情况下，明星分析师会选择偏离均衡（因为无论投资者在观测到标新立异的观点时选择何种策略，明星分析师均会获得更高的收益）。

因此，该博弈不存在混同纯策略纳什均衡。

②分离纯策略纳什均衡。

若明星分析师与一般分析师在均衡时的策略分别为（发表标新立异的观点，发表跟风的观点），投资者接收到发表标新立异的观点的分析师为明星分析师而发表跟风的观点的分析师为一般分析师的信号。此时，有p＝1，q＝0。在此情况下，投资者选择采纳明星分析师的标新立异的观点的期望收益αUe大于不采纳明星分析师的标新立异观点的期望收益（1－α）Ue。因此，投资者选择采纳明星分析师标新立异的观点。同时，投资者选择不采纳一般分析师跟风的观点的期望收益αUf大于采纳一般分析师跟风的观点的期望收益（1－α）Uf。因此，投资者选择不采纳一般分析师跟风的观点。

给定投资者的策略选择，明星分析师不会选择偏离均衡的策略（因为在偏离均衡的情况下，投资者不会采纳明星分析师的观点，明星分析师获得的收益更低），一般分析师同样不会选择偏离均衡的策略（因为在偏离均衡的情况下，一般分析师获得的收益更低）。

明星分析师发表标新立异的观点，一般分析师发表跟风的观点，投资者采纳标新立异的观点而不采纳跟风的观点，是该博弈的一个分离纯策略纳什均衡。

若明星分析师与一般分析师在均衡时的策略分别为（发表跟风的观点，发表标新立异的观点），投资者接收到发表标新立异的观点的分析师为一般分析师而发表跟风的观点的分析师为明星分析师的信号。此时，有p＝0，q＝1。在此情况下，投资者选择采纳明星分析师跟风的观点的期望收益（1－α）Uf小于不采纳明星分析师跟风的观点的期望收益αUf。因此，投资者选择不采纳明星分析师的跟风观点。同时，投资者选择采纳一般分析师标新立异的观点的期望收益αUe大于不采纳一般分析师标新立异的观点的期望收益（1－α）Ue。因此，投资者选择采纳一般分析师标新立异的观点。

给定投资者的策略选择，明星分析师会选择偏离均衡的策略（因为在偏离均衡的情况下，投资者会采纳明星分析师的观点，明星分析师获得的收益更高），一般分析师同样会选择偏离均衡的策略（因为在偏离均衡的情况下，一般分析师获得的收益更高）。该均衡不存在。

综上所述，［（发表标新立异的观点，发表跟风的观点），（采纳观点，不采纳观点），p＝1，q＝0］为上述博弈的分离纯策略纳什均衡。在该分离纯策略纳什均衡下，明星分析师选择发布标新立异的观点而一般分析师选择发表跟风的观点，投资者在观测到标新立异的观点时选择采纳观点，而不采纳跟风观点，投资者的信念为发表标新立异观点的分析师100%是明星分析师，发表跟风观点的分析师100%是一般分析师。

4．1．2．4　博弈模型比较及总结

以上各博弈模型对从多角度认识分析师竞争行为及其与投资者互动具有重要意义。分析师行为价值函数下的静态博弈模型从不同分析师的效用函数出发，刻画分析师在均衡时的行为特征，该模型虽然能够较为贴切地刻画明星分析师与一般分析师的行为特征，但却忽略了在实际决策过程中分析师发布估值报告的择时行为。为了弥补静态博弈模型的不足，引入分析师依次决策下的序贯博弈，考察一般分析师在明星分析师之后发布研究报告的行为，且在模型中引入市场噪音。该序贯博弈模型能够较为贴切地模拟市场中明星分析师与一般分析师的决策行为，且将分析师个人效用函数与分析师预测偏误挂钩，模拟分析师实际生活中的绩效考核行为，然而该序贯模型仅考察了分析师个体行为，而忽略了投资者行为及其影响。为了刻画个人投资者在决策中的相对信息缺失，引入投资者仅知道市场中明星分析师与一般分析师分布但无法辨别其类型的信号博弈模型，考察在均衡时投资者的信念及其行为以及不同分析师的预测行为。在该信号博弈的均衡条件下，明星分析师更倾向于发表标新立异的观点，而一般分析师更倾向于跟风，这与静态模型、序贯博弈模型的结果相一致。但该模型设定中仅考虑了分析师效用的相对大小，并未考虑分析师效用函数的决定方式与影响因素。此外，上述各模型仅考察了局中人单期的策略及决策过程，而实际过程中往往是多期的重复博弈过程，在多期博弈过程中，分析师及投资者的策略集更为复杂，但上述模型至少从单期的角度刻画了分析师和投资者的博弈过程，对理解在竞争非均势情形下的分析师个体行为特征具有重要参考价值。