考虑一个依据分析师预测的准确度历史更新权重的模型，在t时刻预测t＋1时刻的股票价格。参与人及其决策过程与基本模型一致。与基本模型不同的是，在投资者决策过程中，投资者并非依照明星分析师和一般分析师占比加权来确定对市场价格的预期，而是根据不同类别的分析师预测的准确度更新权重，即投资者观察到证券分析师上一期预测的价格与市场最终实现的价格间的差距后，对分析师的可信度赋予一定的权重，并以此作为下一期股票市场价格预期的参考。因此，投资者对股票价格的预期满足：

其中，pt表示第t期投资者对不同类型分析师提供的预测价格赋予的权重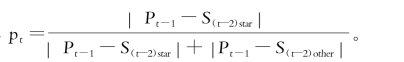

由于pt在第t期投资者决策时为给定值，因此，引入分析师竞争机制的模型对投资者的决策几乎不会产生影响，但对分析师收益的实现及股票市场价格的波动会产生重要影响。假设投资者对所有分析师给予相同的报酬，将其标准化为1，明星分析师在每期所获得的收益为：pt×1/p＝pt/p，一般分析师在每期所获得的收益为：（1－pt）×1/（1－p）＝（1－pt）/（1－p）。分析师每期所获得的收益与上期分析师预测的相对准确度相关。当pt＞p时，明星分析师当期获得的收益相对高于一般分析师；当pt＜p时，一般分析师当期获得的收益相对高于明星分析师，即分析师会因为上期相对更高的预测准确度在本期获得更多的收益。此外，当期股票价格的波动满足：

与式（3-16）相比，存在分析师更新权重的模型下的股票价格波动更加复杂，与当期投资者决策时的权重高度相关，当期被投资者相对更为看重的分析师预测准确度的分布对当期股票市场价格的波动具有相对更重要的影响。(www.daowen.com)

处于稳态时，有Var（Pt）＝Var（Pt＋1），即存在pt＝pt＋1＝p*，对所有t均成立。在此情况下，明星分析师的预测误差与一般分析师的预测误差满足：

即明星分析师的预测误差与一般分析师的预测误差之比满足一个不随时间变化的固定值。