（1）模型设定。

在参考De Long等（1990）以及Jegadeesh和Kim（2010）模型的基础上^[1]，考虑一个t预测t＋1时刻的股票价格、包含多方市场主体的两期模型。参与人包括两类分析师（明星分析师和一般分析师）、上市公司以及两类投资者（噪音交易者和知情交易者）。投资者在t时具有w的财富禀赋，其在投资股票和无风险资产间权衡，投资无风险资产的预期收益率为r。

（2）参与人决策过程。

步骤1：上市公司发布影响公司股票价格的信息。

步骤2：两类分析师通过不同的渠道获得上市公司的相关信息：明星分析师通过上市公司内部渠道获得上市公司的相关信息，一般分析师通过公开信息披露渠道获得上市公司的相关信息。

步骤3：分析师根据自身获得的信息分析并发布对该上市公司的研究报告。

步骤4：投资者在观测到分析师发布的研究报告后，进行投资决策。

步骤5：股票价格的实现。

假设上市公司的真实内在价值为，私有信息提供的关于上市公司价值的信息与上市公司的真实内在价值间满足：

公开信息提供的关于上市公司价值的信息与上市公司的真实内在价值间满足：

其中，ε～

鉴于明星分析师通过私有信息进行预测，其对私有信息的解读存在误差ξ～N（0，明星分析师预测的股票价格：

一般分析师通过公开信息进行预测，其对公开信息的解读存在误差υ～N（0一般分析师预测的股票价格：

由于明星分析师与一般分析师信息解读能力间存在差异，有

（3）投资者进行投资决策的过程。

噪音交易者对股票价格的判断偏误ρ服从ρ投资者效用函数：

其中，γ衡量了投资者的风险厌恶程度，w表示投资者的财富水平。

由于投资者财富水平服从正态分布，投资者的效用水平服从对数正态分布，则知情交易者的期望效用：

其中表示知情交易者投资股票的财富占比。

对应的噪音交易者的期望效用：

其中表示噪音交易者投资股票的财富占比。

最大化投资者的期望效用函数，可以得出：

由于市场中噪音交易者的测度为μ，知情交易者的测度为1－μ，则有：

由此可得出市场价格的决定方程：

投资者对市场价格的预期来源于阅读证券分析师的报告，假设市场上明星分析师的占比为p，一般分析师的占比为1－p。投资者采取的策略为依照明星分析师和一般分析师占比加权来确定对市场价格的预期，即：

则有实际股票价格满足：

各参数对当期股票市场价格的影响如下。

①无风险资产收益率r的变化对股票市场的影响较为复杂，取决于各变量间的大小关系。

②投资者的风险厌恶程度越高，γ越大，股票的当期市场价格越低。

③上市公司股票价格的波动性越大越高，股票的当期市场价格越低。

④市场上噪音交易者越多，μ越大，股票的当期市场价格越高。

⑤噪音交易者对当期信心越高，ρt越大，股票的当期市场价格越高。

⑥市场传递信息的正向偏误（ε，η＞0）、分析师预测的正向误差（ξ，υ＞0）越大，股票的当期市场价格越高；市场传递信息的负向偏误（ε，η＜0）、分析师预测的负向误差（ξ，υ＜0）越大，股票的当期市场价格越低。

对式（3-13）两边同取期望，有：

股票市场预期与上市公司股票的内在价值间的差异由式（3-15）决定：

式（3-15）表明：(www.daowen.com)

①当p（ε＋ξ）＋（1－p）（η＋υ）＞0时，市场预期的股票价格高于上市公司股票的内在价值。

②当p（ε＋ξ）＋（1－p）（η＋υ）＜0时，市场预期的股票价格低于上市公司股票的内在价值。

③当p（ε＋ξ）＋（1－p）（η＋υ）＝0时，市场预期的股票价格等于上市公司股票的内在价值。

对式（3-11）两边同取方差：

式（3-16）表明，分析师与投资者特征将在如下几个方面影响股票价格波动。

①明星分析师占比与Pt波动间呈现U型关系。当明星分析师占比p较小时，Pt的波动随着明星分析师占比的升高而降低；当明星分析师占比较高时，Pt的波动随着明星分析师占比的升高而升高。

②分析师预测误差的波动越大越大），信息的传递效率越低越大），Pt波动越大。

③μ越大，市场上噪音交易者占比越多，Pt波动越大。

④越大，即噪音交易者对股票价格预测分歧越大，Pt波动越大。

（4）分析师收益的实现。

假设投资者对所有分析师给予相同的报酬，将其标准化为1，明星分析师在每期所获得的收益为：p×1/p＝1，一般分析师在每期所获得的收益为：（1－p）×1/（1－p）＝1。

（5）稳态求解。

假设市场在t＋1期及其之后达到稳态，满足条件E（Pt＋1）＝E（Pt＋2），Var（Pt＋1）＝Var（Pt＋2），则有：

其中，Var（Pt＋1

因此，当期的价格由下式决定：

在市场t＋1期及其之后达到稳态的情形下，当期市场价格主要受到市场中明星分析师占比p、市场信息传递效率、分析师解读信息能力市场中噪音交易者占比μ、噪音分布以及当期噪音特征ρt决定。其影响方向和大小如下。

①明星分析师占比对价格的影响。

明星分析师占比对价格的影响方向取决于的相对大小。当明星分析师占比的增加会使得市场价格降低，当明星分析师占比的增加会使得市场价格上升。

②市场信息传递效率与分析师解读信息能力对价格的影响。

市场信息传递效率越高，分析师解读信息能力越强，即越小，市场价格越低。

③市场中噪音交易者占比对价格的影响。

市场中噪音交易者占比的变动对市场价格的影响方向较为复杂，主要与噪音的分布特征相联系。

④噪音分布均值对价格的影响。

噪音分布的均值越高，噪音交易者的乐观偏差越大，市场价格越高。

⑤噪音分布方差对价格的影响。

噪音分布的波动越大，市场价格越低。

⑥当期噪音特征对价格的影响。

当期噪音水平越高，对市场预期的乐观偏差越大，市场价格越高。

（6）投资者收益差异。

噪音交易者与知情交易者间收益的差异满足：

其中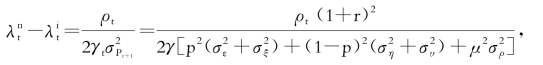若当期噪音交易者对市场价格存在乐观偏差（即ρt＞0），则噪音交易者将比知情交易者投资更多的风险资产。

风险资产的超额收益由投资者的风险厌恶程度γ、市场中明星分析师占比p、市场中噪音交易者占比μ以及当期噪音特征ρt等因素综台决定。

因此，噪音交易者与知情交易者间期望收益的差异：

即噪音交易者与知情交易者的期望收益间存在一定的差异，且该差异与噪音的偏误ρ*间呈现一个开口向下的抛物线。该抛物线的顶点位于：

其符号由各参数的相对大小决定。因此，噪音交易者与知情交易者的相对收益并不确定。但该抛物线的形状至少表明，在多数情况下，噪音交易者的期望收益低于知情交易者的收益，噪音交易者在交易中往往会受损。