标准的M/M/c模型的各种特征的规定与标准的M/M/1模型的假设相同，另外假设各服务台工作是相互独立的，且平均服务率相同，即µ1=µ2=···=µc=µ。这样，当n≥c时，整个服务机构的平均服务率为cµ；而当n<c时，整个服务机构的平均服务率为nµ。令只有当ρ<1时不会排成无限的队列，称它为这个系统的服务强度或称服务机构的平均利用率。该系统的图示如图11-11所示。

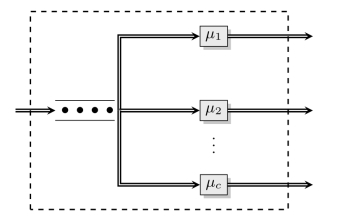
图11-11　标准的M/M/c模型

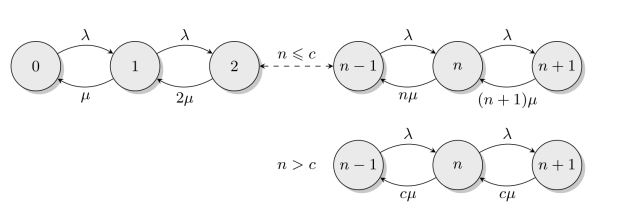
图11-12　标准的M/M/c模型的生灭过程

该系统的生灭过程如图11-12所示。状态1转移到状态0时，即系统中有一名顾客被服务完了的转移率为µP1，状态2转移到状态1时，这就是在两个服务台上被服务的顾客中有一个被服务完成而离去，这时状态的转移率为2µP2。同样，对状态n转移到n-1的情况，若n≤c时，状态转移率为nµPn；当n>c时，因为只有c个服务台，最多有c个顾客在被服务，n-c个顾客在等待，因此这时状态转移率为cµPn。

根据上述生灭过程，得到系统状态转移方程为

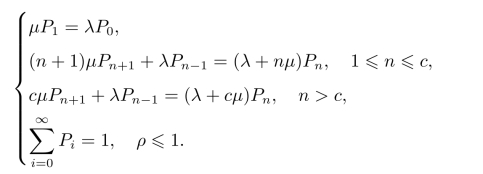
利用递推法求得状态概率为

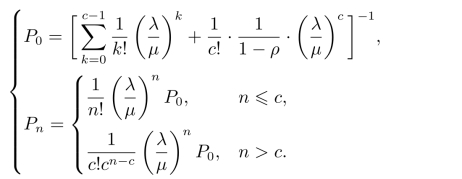
进而得到系统的运行指标为

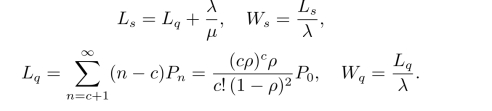
例11.4某售票处有三个窗口，顾客的到达服从泊松过程，平均到达率λ=0.9人/分钟，服务时间服从负指数分布，平均服务率为µ=0.4人/分钟。现顾客到达后排成一队，依次向空闲的窗口购票。求

(1)整个售票处空闲的概率；(www.daowen.com)

(2)系统运行指标；

(3)顾客到达后必须等待的概率。

(1)整个售票处空闲的概率为

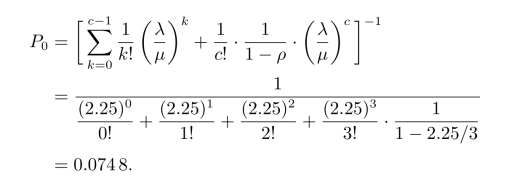
(2)系统运行指标

(3)顾客到达后必须等待的概率为

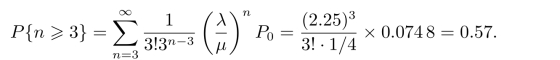
在上面的例子中，如果原题除排队方式外其他条件不变，但顾客到达后在每个窗口前各排一队，且进入队列后坚持不换，这就形成了3个M/M/1模型队列，每个队列的平均到达率为λ1=λ2=λ3=0.3。两类模型的运行指标的对比如表11.6所示。

表11.6　M/M/3模型与M/M/1模型的比较

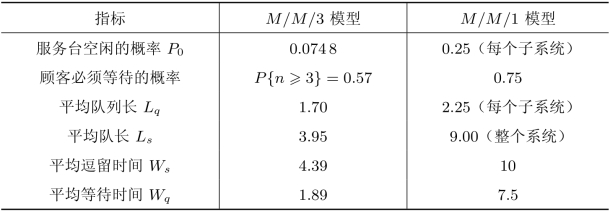
从表11.6中各指标的对比可以看出单队比多队有显著优越性，在安排排队方式时应注意选择适当的排队方式。