M/M/1/∞/m模型表示顾客到达与服务时间均服从负指数分布，单服务台，且顾客源有限的情况。典型的例子如机器因故障停机待修的问题。设共有m台机器，机器因故障停机表示“到达”，待修的机器形成队列，修理工人是服务员。由于同一台机器出故障并经修好后，仍可再出故障，如图11-9所示，所以系统的容量不会超过m，所以与写成M/M/1/m/m没有区别。

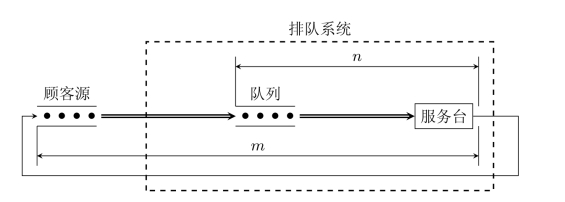
图11-9　M/M/1/∞/m模型图示

对于M/M/1/∞/m模型，设各个顾客的到达率都是相同的λ，这时在系统外的顾客平均数为m-Ls，所以系统的有效到达率就为

与前述分析思路类似，M/M/1/∞/m模型的系统状态稳态情况下的生灭过程如图11-10所示。

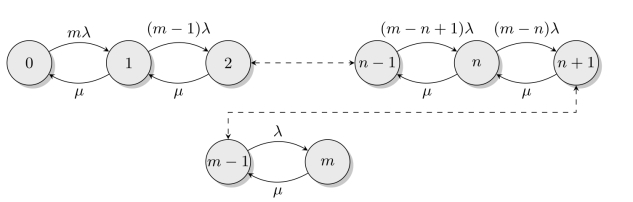
图11-10　M/M/1/∞/m模型的生灭过程

在稳态情况下，当由状态0转移到状态1时，每台设备由正常状态转移为故障状态，其转移率为λP0，现有m台设备由无故障状态转移为有一台设备发生故障，其转移率为mλP0。由状态1转移到状态0，其状态转移率为µP1，所以在状态0时有平衡方程mλP0=µP1。依次类推，可以得到如下状态间转移的差分方程：

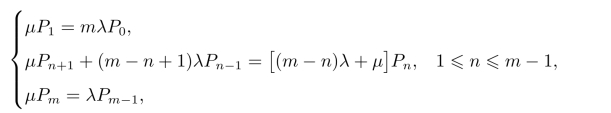
且存在

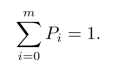
利用递推方法，可以得到系统状态的概率为

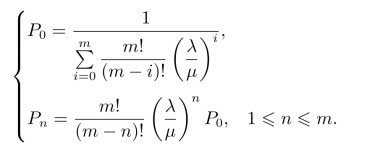
进而可以求得系统运行指标为

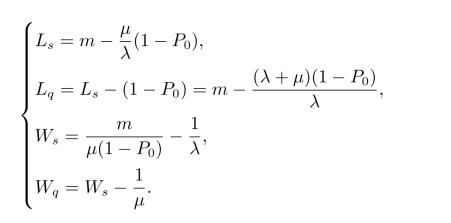
例11.3某车间有5台机器，每台机器的连续运转时间服从负指数分布，平均连续运转时间15分钟，有一名修理工，每次修理时间服从负指数分布，平均每次12分钟。求

(1)修理工空闲的概率；

(2)5台机器都出故障的概率；(www.daowen.com)

(3)出故障的平均台数；

(4)等待修理的平均台数；

(5)平均停工时间；

(6)平均等待修理时间。

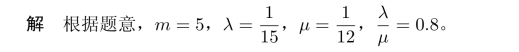
(1)修理工空闲的概率

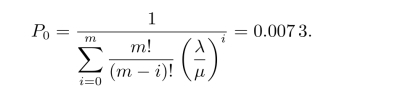
(2)5台机器都出故障的概率

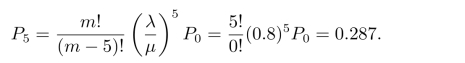
(3)出故障的平均台数

(4)等待修理的平均台数

(5)平均停工时间

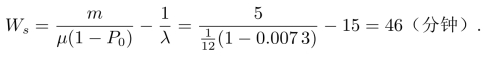
(6)平均等待修理时间

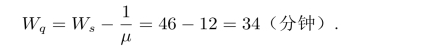
从上述参数来看，机器停工时间较长，修理工几乎没有空闲时间，应当提高服务率减少修理时间或增加修理工人。