M/M/1/N/∞模型表示，系统的最大容量为N，而且为单服务台，这样排队等待的顾客最多为N-1个。在某一时刻，顾客到达排队系统，若系统中已有N个顾客，该顾客则被拒绝进入系统，该排队系统如图11-7所示。显然，当N=1时为即时制的情形；当N→∞时为容量无限制的情况。该系统的生灭过程如图11-8所示。

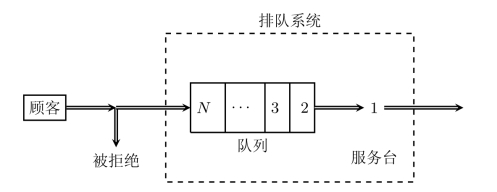
图11-7　M/M/1/N/∞模型图示

图11-8　M/M/1/N/∞模型的生灭过程

由图11-8可得该排队系统的系统状态概率的稳态方程为

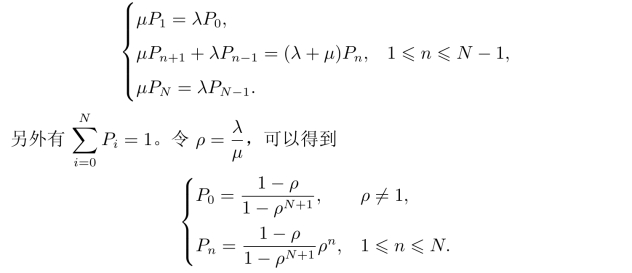
容易知道，当ρ=1时，系统状态为均匀分布。在对容量没有限制的情况下，要求ρ<1，这不仅是实际问题的需要，也是无穷级数收敛的需要。在容量为N时，这个条件就不是必需的了。但当ρ>1时，表示损失率PN（或表示被拒绝进入排队系统的顾客平均数λPN）将会很大。

与前述方法类似，可以得到该排队系统的运行指标如下：

(1)队长期望值

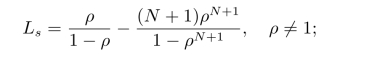
(2)队列长期望值

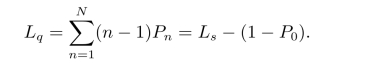
当研究顾客在系统平均逗留时间Ws和在队列中平均等待时间Wq时，注意平均到达率λ是在系统中有空时的平均到达率，当系统已满时，则到达率为0，因此需要求出有效到达率λe=λ(1-PN)，可以验证

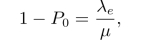
所以

(3)顾客逗留时间期望值

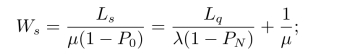
(4)顾客等待时间期望值(www.daowen.com)

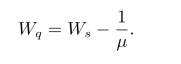
例11.2单人理发店有6个椅子接待人们排队等待理发。当6个椅子都坐满时，后来的顾客不进店就离开。顾客平均到达率为3人/小时，理发需时平均15分钟。求

(1)某顾客一到达就能理发的概率；

(2)需要等待的顾客数的期望值；

(3)有效到达率；

(4)一顾客在理发店逗留的期望时间；

(5)到达的顾客不等待就离开的概率。

解根据题意，λ=3人/小时，µ=4人/小时，N=7。

(1)某顾客一到达就能理发，意味着理发店没有顾客，即

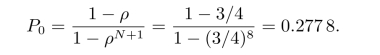
(2)需要等待的顾客数的期望值为

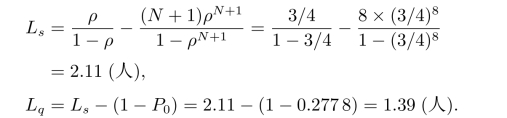
(3)有效到达率

(4)一顾客在理发店内逗留时间的期望值为

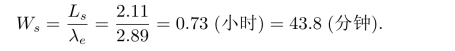
(5)到达的顾客不等待就离开的概率，即系统中有7个顾客的概率

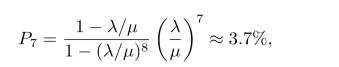
这也是理发店的顾客损失率。