标准的M/M/1模型的假设包括：

(1)输入过程——顾客源是无限的，顾客单个到来，相互独立，一定时间的到达数服从参数为λ的泊松分布，到达过程是平稳的；

(2)排队规则——单队，且对队长没有限制，先到先服务；

(3)服务机构——单服务台，各顾客的服务时间是相互独立的，服从相同的负指数分布，参数为µ；

(4)到达间隔时间和服务时间是相互独立的。

为了分析系统运行特征，首先需要确定系统状态的分布。在时间区间[t,t+Δt)内系统状态如表11.3所示（到达或离去两个或两个以上顾客的情况未列出）。

表11.3　M/M/1模型不同的系统状态

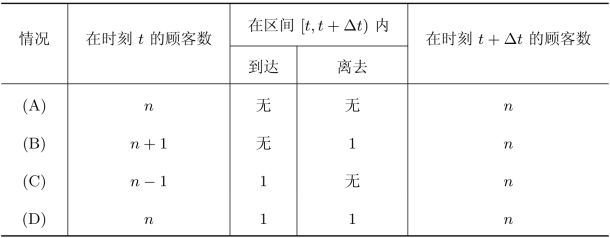
由于到达过程为泊松分布，服务时间为负指数分布，所以在时间区间[t,t+Δt)内，

(1)有1个顾客到达的概率为λΔt+o(Δt)，没有顾客到达的概率为1-λΔt+o(Δt)；

(2)当有顾客在接受服务时，1个顾客被服务完了离去的概率是µΔt+o(Δt)，没有离去的概率为1-µΔt+o(Δt)；

(3)多于一个顾客的到达或离去的概率是o(Δt)，可以忽略。

这样，表11.3中的4种情况的概率分别为（略去了o(Δt)项）：

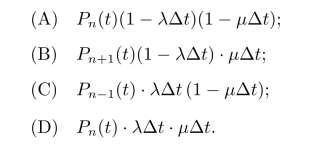
由于这4种情况是互不相容的，所以Pn(t+Δt)应是这4项之和（合并了o(Δt)项）：

整理后可以得到

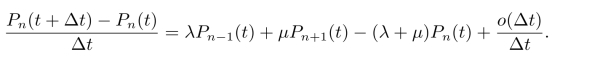
令Δt→0，得到关于Pn(t)的微分差分方程为

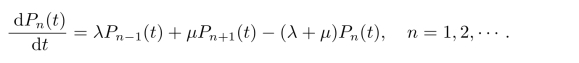
此外，当n=0时，有

类似地可以得到

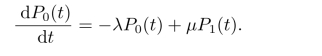
解上述微分差分方程可以得到系统的瞬态解，但如前所述瞬态解的现实应用意义不大，所以我们只求其稳态解，此时Pn(t)与t无关，用Pn表示，它的导数为0，这样前述的微分差分方程变为

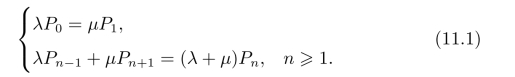
该方程组是关于Pn的差分方程，它表明了各状态间的转移关系，可用生灭过程描述如图11-6所示。

根据生灭过程的平衡状态，同样可以得到(11.1)式所示的差分方程组。由(11.1)式可得

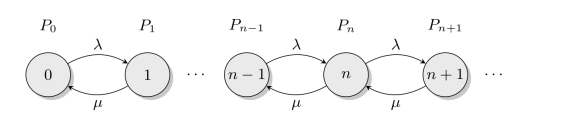
图11-6　M/M/1模型的生灭过程

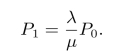
当n=1时，可以得到

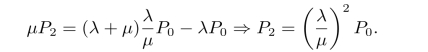
同理依次可得

以(11.2)式为基础，可以得到M/M/1系统的运行指标：(www.daowen.com)

(1)在系统中的平均顾客数（队长期望值）

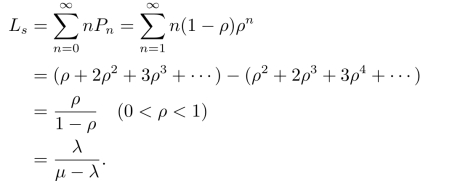
(2)在队列中等待的平均顾客数（队列长期望值）

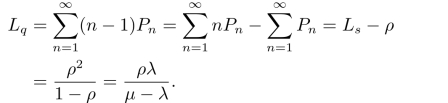
(3)顾客在系统中的逗留时间W为一随机变量，在M/M/1模型中，它服从参数为µ-λ的负指数分布，即

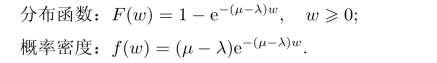
这样可以得到在系统中顾客逗留时间的期望值为

在队列中顾客等待时间的期望值为

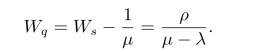
现将以上各式归纳如下：

它们之间的关系为

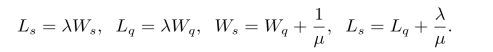
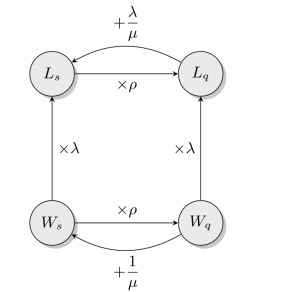
上式称为Little公式，也可以用下图表示：

例11.1某医院手术室根据病人来诊以及完成手术时间的记录，任意抽查了100个工作小时，每小时来就诊的病人数n的出现次数如表11.4所示。又任意抽取了100个完成手术的病历，所用时间v（小时）出现的次数如表11.5所示。试根据上述数据计算该服务系统的运行指标。

表11.4　病人到达情况

表11.5　手术时间情况

解假设病人到达服从泊松过程，手术时间服从负指数分布。根据表11.4和表11.5可以得到，每小时病人平均到达率

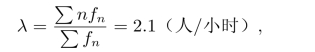
每小时完成手术人数为

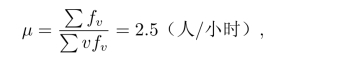
所以，

即说明，手术室有84%的时间处于繁忙状态，有16%的时间处于空闲中。同时，在病房中的病人数的期望值为

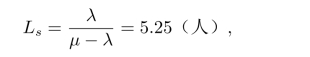
排队等待手术的病人数的期望值为

病人在手术室逗留时间的期望值为

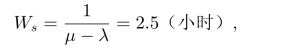
病人排队等候治疗的时间期望值为