设N(t)为在时间区间[0,t)内到达的顾客数（t>0），Pn(t1,t2)表示在时间区间[t1,t2)(t1<t2)内有n(≥0)个顾客到达的概率，即

Pn(t1,t2)的分布可能呈现多种形态，但现实中最为常用的是泊松输入过程。当Pn(t1,t2)满足下列三个条件时，我们说顾客的到达过程为泊松输入过程：

(1)在不相重叠的时间区间内顾客到达数是相互独立的，即输入过程满足无后效性；

(2)对充分小的Δt，在时间区间[t,t+Δt)内有1个顾客到达的概率与t无关，而与时间区间长度Δt成正比，即

其中o(Δt)当Δt→0时是关于Δt的高阶无穷小；λ>0是常数，它表示单位时间有一个顾客到达的概率，称为概率强度；

(3)对于充分小的Δt，在时间区间[t,t+Δt)内有2个顾客或2个以上顾客到达的概率极小，可以忽略，即

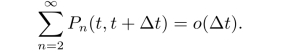
根据上述条件，可以确定顾客到达数的概率分布。根据条件(2)，总可以取初始时间为0，并简记Pn(0,t)=Pn(t)。而且容易得到在[t,t+Δt)区间内没有顾客到达的概率为

区间[0,t+Δt)可以分为两个互不重叠的区间[0,t)和[t,t+Δt)，若[0,t+Δt)内顾客到达的总数为n，则可能出现如表11.2所示的三种情况。

表11.2　[0,t+Δt)区间内到达n个顾客的情况(www.daowen.com)

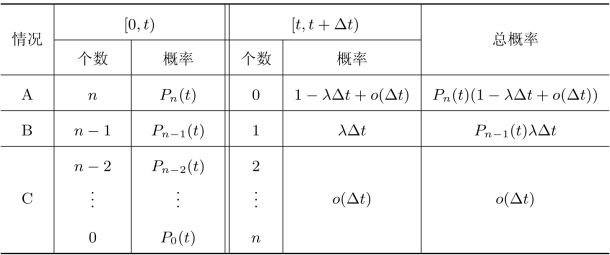
由于[0,t+Δt)区间内到达n个顾客的三种情况互不相容，所以

整理得

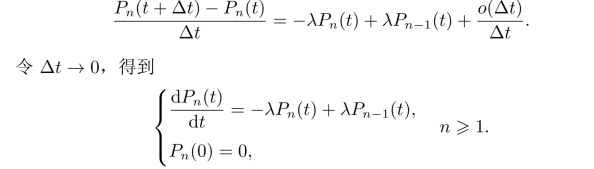
当n=0时，没有B,C两种情况，所以有

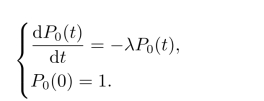
求解后可以得到

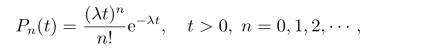
此即为长为t的时间区间内到达n个顾客的概率。所以，随机变量{N(t)=N(s+t)-N(s)}的数学期望与方差分别为

期望值与方差相等，是泊松输入过程的一个重要特征，也可以利用这一性质对一个经验分布是否属于泊松输入过程进行初步的识别。