在该模型中，货物单位成本为K，货物单位售价为P，单位存储费用为C1，需求r是连续的随机变量，概率密度函数为f(r)，这样f(r)dr表示随机变量在r与r+dr之间的概率，其分布函数为F(a)=∫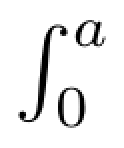f(r)dr(a>0)，生产或订购的数量为Q，为决策变量。

当订购数量为Q时，实际销售量应该是min{r,Q}，也就是当需求为r，而r小于Q时，实际销售量为r；当r≥Q时，实际销售量只能是Q。该模型中的存储费用为

货物的成本为KQ，本阶段订购量为Q，赢利为W(Q)，赢利的期望值记为E[W(Q)]。

本阶段的赢利为实际销售收入与货物成本和存储费用之差，即

为使得赢利期望值最大，有下列等式：

或

上面两式表明，赢利最大和损失极小所得出的Q是相同的，而且两者期望值之和为一常数。这样，求赢利极大可以转化为求损失极小。当Q可以连续取值时，E[C(Q)]是Q的连续函数，可利用一阶导数条件求其最小值，即令

得到(www.daowen.com)

进而得到

由上式即可解出Q，记其为Q∗，即为模型的最小值点。

此外，若P-K≤0，显然由于F(Q)≥0，等式不成立，此时Q∗取零值，即售价低于成本时，不需要订货。

前述过程只考虑了失去销售机会的损失，如缺货时需付出的费用C2>P时，应用

按上述推导过程可得

另外，模型五及模型六都只解决了一个阶段的问题，从一般情况来看，上一个阶段未售出的货物可以在第二个阶段继续出售，这时的存储策略如下：

这种策略也可以称为定期订货，订货量不定的存储策略。