在前述的模型中，由于货物单价是一确定量，所以得到的最优存储策略与货物的单价无关。但在现实中如果货物单价是变化的，如常见的量大从优的情况，这时就必须考虑货物单价对存储策略的影响了。下面主要讨论价格有折扣的存储问题，其他类似问题可以借鉴这一思路。

令货物单位为K(Q)，且K(Q)按三个数量等级变化，

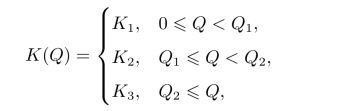
这是一个阶梯函数，如图10-8所示。

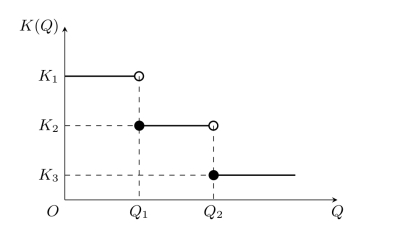
图10-8　阶梯型货物单价

当订货量为Q时，一个周期内所需费用为

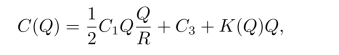
即

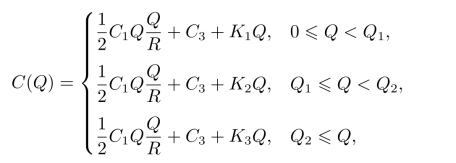
平均每单位货物所需费用为

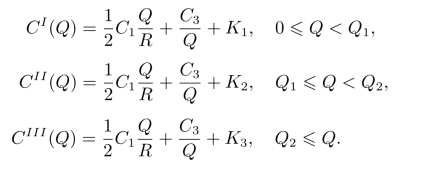
上述成本函数如图10-9所示。

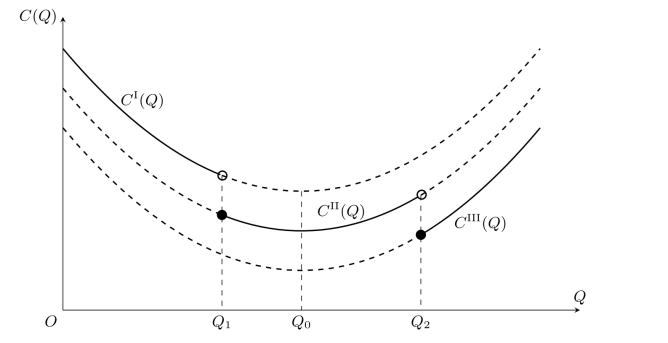
图10-9　单位货物的费用

如果不考虑CI(Q),CII(Q),CIII(Q)的定义域，它们之间只差一个常数，因此它们的导函数是相同的。为求得极小值，令导数为0，可以解得Q0，但该值落在哪一个区间，事先无法确定。(www.daowen.com)

假设Q1<Q0<Q2，这也不肯定CII(Q)就是最小的。由图10-9可知，CIII(Q2)的值可能更小。所以，如果设最佳订购批量为Q∗，在给出价格有折扣的情况下，求解步骤如下：

(1)对CI(Q)求得极值点为Q0（不考虑定义域）。(2)若Q0<Q1，计算

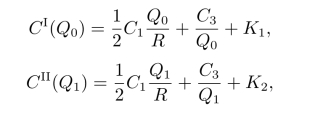
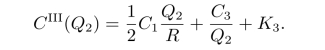
由min{CI(Q0),CII(Q1),CIII(Q2)}得到单位货物最小费用的订购批量Q∗。

(3)若Q1≤Q0<Q2,计算CII(Q0),CIII(Q2),由min{CII(Q0),CIII(Q2)}决定Q∗。

(4)若Q2≤Q0，则Q∗=Q0。

例10.3某报社必须定期补充纸张的库存量，假定新闻纸以大型卷筒进货。每次订货费用为25元，纸张的价格按下列进货批量进行折扣：买1～9筒，单价为12元；买10～49筒，单价为10元；买50～99筒，单价为9.5元；买100筒以上，单价为9元；另外，车间的消耗为每周32筒，存储纸张的费用为每周每筒1元。求最佳订货批量和每周的最小费用。

解由题设条件可知，R=32，C1=1，C3=25，由经济订购批量公式可得

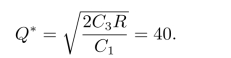
因为Q0落在10～49之间，每筒的价格为10元，所以每周的平均费用为

而可以计算得到

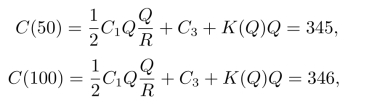
所以最佳订货批量应为50筒，费用为345元/周。