该模型的假设条件除允许缺货和生产需一定时间外，其余条件与模型一相同，其存储量变化如图10-7所示。

图10-7　模型四存储量变化示意图

图10-7中，t为一个周期，假设从0时刻开始，存储量为0。t1时刻开始生产，t3时刻停止生产。存储量的变化过程如下：

[0,t1]时间内存储量为0，存储系统处于缺货状态，需求速度为R。设B为最大缺货量，则有B=Rt1。

[t1,t2]时间内，企业开始生产，一方面需满足当前需求，同时需补足[0,t1]时间内的缺货，所以存储量仍然为0，但存在B=(P-R)(t2-t1)。

[t2,t3]时间内，由于生产速度高于需求速度，存储量以P-R的速度开始增加。若用S0表示最大存储量，则S0=(P-R)(t3-t2)。

[t3,t]时间内，企业在t3时刻停止生产，系统存储量开始以R的速度减少，到时刻t时存储量回到0，完成一个周期。同样可以得到S0=R(t-t3)。

从上述分析过程中可以发现，由于存在B=Rt1=(P-R)(t2-t1)，所以可以得到

另外，由于S0=(P-R)(t3-t2)=R(t-t3)，所以

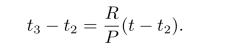
下面讨论在[0,t]时间内的所有费用：

装配费：C3(www.daowen.com)

这样，在[0,t]时间内总平均费用为上述三项费用之和除以周期时间，即

为求得上式的最小值，令

得到

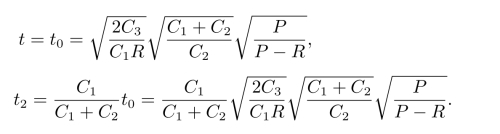
由此可以得到该模型的其他参数分别为订货量

最大存储量

最大缺货量

最低费用为