在该模型中,假设:
(1)不允许缺货,即认为缺货费用为无穷大;
(2)当存储量降至0时,可以立即得到补充,即不考虑备货时间;
(3)需求是连续的、均匀的,即若需求速度为R,则t时间内的需求量为Rt;
(4)每次订货量固定,订购费用不变;
(5)单位存储费用不变。
该模型是存储论中最基本的模型,也是最简单的模型,该存储系统中存储量的变化情况如图10-3所示。
一个好的存储策略应使得系统的总费用最低,通常有两种思路来实现这一目标。一是使每个订货周期内的单位时间费用最低,另一种是使每个订货周期内的单位货物费用最少。实际上,这两种方法是等效的。

图10-3 模型一存储量变化示意图

所以上述t0值使得C(t)最小,即每隔t0时间订货一次可使C(t)最小,订货批量为

上式就量存储论中著名的经济订货批量公式(Economic Ordering Quantity,EOQ),也称为平方根公式或简称为经济批量公式。
由于Q0,t0皆与货物单价K无关,所以此后在货物单位为既定常数时,可在费用函数中略去KR这项费用。这样模型一的费用函数为

也可根据费用函数曲线来求解模型一的最优存储策略,如图10-4所示。
 (https://www.daowen.com)
(https://www.daowen.com)
图10-4 模型一的总费用示意图

上述分析结果是基于订货周期作为决策变量得到的,如果选取订货批量Q作为决策变量也可以得到同样的结果。首先,一个订货周期内单位货物的存储费用为

一个订货周期内单位货物的订货费用为
![]()
则单位货物的总费用为

利用一阶导数条件求其最小值,得到

例10.1若某产品中有一外购件,年需求量为10 000件,单价为100元。由于该件可在市场采购,故订货提前期为零,并设不允许缺货。已知每组织一次采购需2 000元,每件每年的存储费为该件单价的20%,试求经济订货批量及每年最小的存储加上采购的总费用。
解根据题意可知,R=10 000,C3=2 000,C1=20,且不允许缺货,备货时间很短,符合模型一的假设条件,所以经济订货批量为

订货周期为

最小总费用为
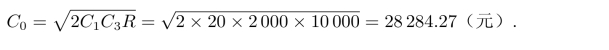
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






