图解法适用于赢得矩阵为2×n或m×2型的对策问题。首先看2×n矩阵对策问题的图解方法。

例9.7(混合策略的图解法)求下面矩阵对策问题的解：

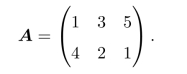
解首先判断这个矩阵对策问题已经最简化了，而且不存在纯策略意义上的解。

设局中人I的混合策略为(x,1-x)T。过数轴上为(0,0)和(1,0)点分别作两条垂线I-I和II-II，垂线上点的纵坐标值分别表示局中人I采取纯策略α1和α2时，局中人II采取各纯策略时的赢得值，如图9-1所示。当局中人I选择每一策略(x,1-x)T时，他的最少可能的收入为局中人II选择β1,β2,β3时所确定的三条直线：

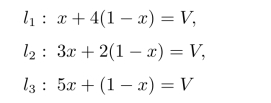
在x处的纵坐标中最小者，即图9-1中折线B1B2BB3所示。

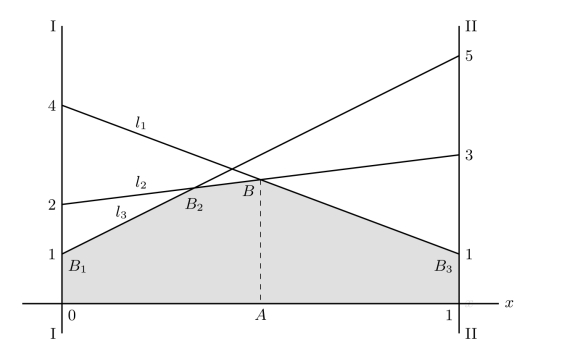
图9-1　2×n矩阵对策的图解法

所以，对局中人I来说，他的最优选择就是确定x使他的收入尽可能地多，从图9-1可知，按最小最大原则应选择x=OA，而AB的长度即为对策值。为求出点x和对策值VG，可联立过B点的两条线段l1和l2所确定的方程组：

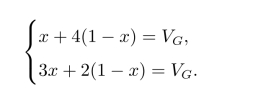(www.daowen.com)

解得x=0.5，VG=2.5。所以，局中人I的最优策略为x∗=(0.5,0.5)T。

解得y∗=(0.25,0.75,0)，VG=2.5为局中人II的最优混合策略与对策值。

对于m×2型的矩阵对策，其图解思路与2×n型类似。

例9.8求下面矩阵对策问题的解：

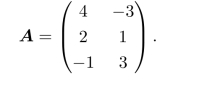
解设局中人II的混合策略为(y,1-y)。作图过程与上例类似，见图9-2。

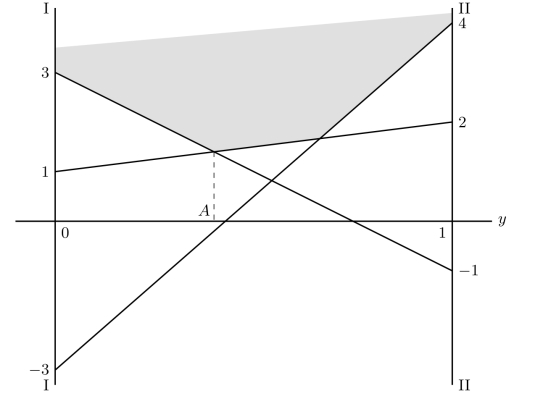
图9-2　m×2矩阵对策的图解法

图9-2中A为y∗，解方程组