当矩阵对策模型确定后，各局中人面临的问题便是如何选择对自己最有利的纯策略，以谋取最大的赢得（或最小损失）。下面通过一个具体例子来分析应如何求解各局中人的最优策略。

例9.4(矩阵对策)设有一矩阵对策G={S1,S2;A}，其中S1={α1,α2,α3}，S2={β1,β2,β3}，且

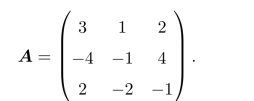
试求双方的最优策略。

解由局中人I的赢得矩阵A可以看出，局中人I的最大赢得是4，要想得到这个赢得，他应选择策略α2。由于局中人II也是理智的，他考虑到局中人I打算选择α2的心理，于是他会准备用β1对付局中人I，使他不仅得不到4反面失去4。由于局中人I也是理智的，当然也会猜到局中人II的这一心理，所以他会用α1来对付，使局中人II得不到4反而失去3……所以，如果双方都不想冒险，都不存在侥幸心理，而是考虑到对方必然会设法使自己的所得最少这一点，就应该从各自可能出现的最不利的情形中选择一种最有利的情形作为决策的依据，这是一种稳妥的方式，也是所谓的“理智行为”。

这样，局中人I的三种策略可能带来的最少赢得，即矩阵A中每行的最小元素分别为1,-4,-2，在这些最少赢得中最好的结果是赢得1。所以，局中人I只要以α1参加对策，无论局中人II选取什么样的策略，都能保证局中人I的收入不会少于1；而出其他任何策略，其收入都有可能少于1，甚至输给对方。同理，对局中人II来说，各策略可能带来的最不利的结果，即矩阵A中每列的最大元素分别为3,1,4，在这些最不利的结果中最好的结果（输得最少）是1。即局中人II只要选择策略β2，无论局中人I采取什么样的策略，都能保证自己的损失不会多于1；而采取其他任何策略，其损失都有可能多于1。

上面的分析表明，局中人I,II的“理智行为”分别是选取纯策略α1和β2，这时局中人I的所得和局中人II的所失相等，均为1。局中人I是按最大最小原则，局中人II是按最小最大原则选择各自的策略，这对双方来说都是一种最为稳妥的行为。因此α1和β2分别为局中人I,II的最优策略。

一般地，对于矩阵对策问题G={S1,S2;A}，其中S1={α1,α2,···,αm}，S2={β1,β2,···,βn}，且A=(aij)m×n，若存在

则VG=ai∗j∗称为对策G的值，称使上式成立的局势(αi∗,βj∗)为G在纯策略下的解，αi∗和βj∗分别称为局中人I,II的最优纯策略。

注意到，根据对策值的定义，它具有这样的特征：它是所在行的最小值，也是所在列的最大值。如例9.4中，对策值VG=1既是第一行的最小值，也是第二列的最大值。另外，这样可使得αi∗和βj∗成为矩阵对策的最优策略，因为此时对策双方都没有动机偏离现有这个策略。如在例9.4中，当局中人II选择β2作为最优策略时，局中人I不会偏离策略α1，不然他的收益会更低，所以α1成为局中人I的最优策略。反过来，当局中人I选择α1作为其最优策略时，局中人II也没动机偏离β2这个策略，不然他损失的会更多，所以β2成为局中人II的最优策略。可见，此时对策处于一种均衡状态，因此局势(αi∗,βj∗)也称为对策的均衡解。

例9.5已知A,B两对策时，A的赢得矩阵如下：(www.daowen.com)

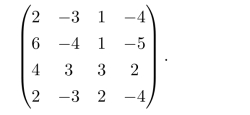
求双方的最优策略及对策的值。

解根据前述定义，对于A的赢得矩阵按行小中取大，按列大中取小，如果它们的值相等且与交叉点的值相等，即可得到对策的最优策略与对策值。将求解过程列于表9.2中。

由此得到，局中人A的最优策略为α3，局中人B的最优策略为β4，对策值VG=2。

上述矩阵对策的思路也可用于某些连续对策问题中。

表9.2　矩阵对策求解

例9.6 A和B进行一种游戏，A先在横坐标x轴的[0,1]区间内任选一个数，但让B知道，然后B在纵坐标y轴的[0,1]区间内任选一个数，双方选定后，B对A的支付为

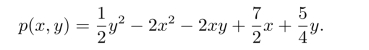
求A,B各自的最优策略和对策值。

解由于分别要对A,B确定其收益极值，所以令