最初用数学方法来研究对策现象的是数家E.Eermelo，他于1912年发表的“关于集合论在象棋对策中的应用”一文中，证明三种着法必定存在一种不依赖黑方（对手）如何行动，白方（自己一方）总取胜的着法，或者黑方总取胜的着法，或者有一方总能保证达到和局的着法（究竟存在的是哪一种并没能指出来）。此后，1921年法国数学E.Borel讨论了个别几种对策现象，并引入了“最优策略”的概念，证明对于这些对策现象存在着最优策略，并猜出了一些结果。1928年，德国数学家von Neumann证明了这些结果。

20世纪40年代以来，由于战争和生产的需要，提出不少“对策问题”，像飞机如何侦察潜水艇的活动、护航商船队的组织形式等。这些问题引起了一些科学家的兴趣，进而对“对策现象”进行了研究，同时许多经济问题使经济学和对策论的研究结合起来，为对策论的应用提供了广泛的场所，也加快了对策论体系的形成。1944年von Neumann和Morgenstern总结了对策论的研究成果，合著了《对策论与经济行为》一书。从此，对策论的研究开始走向系统化和公理化。20世纪50年代，纳什（Nash）建立了非合作博弈的“纳什均衡”理论，标志着博弈论的新时代的开始。

对策是决策主体在他们的策略相互依存情形下相互作用状态的抽象表述，即在对策局势下，各方的利益不仅取决于自身的行为，而且也取决于其他对策参与者的行为。进而言之，一方所采取最优策略取决于他对对手将采取策略的预期，而对策论则是研究上述情况下决策主体的理性行为选择的理论。

在我国古代，“齐王赛马”就是一个典型的对策论研究的例子。战国时期，有一次齐王要与他的大将田忌赛马，双方约定，比赛三局，每局各出赛马一匹，负者要付胜者千金，双方都有上、中、下三个等级的马。已知在同等级的马中，田忌的马不如齐王的马，但如果田忌的马比齐王的马高一等级，则田忌的马就能取胜，如果田忌与齐王的同等级的马比赛，则田忌要连输三局而输掉三千金。当时田忌手下的一位谋士出了一个好对策，每局比赛时先让齐王牵出他的马，然后用下马对齐王的上马，用中马对齐王的下马，用上马对齐王的中马，结果田忌二胜一负，得了千金。这是我国历史上一个最为经典的对策问题。田忌的那位谋士叫孙膑，他后来留下传世的经典著作《孙子兵法》，其中不乏这样对策问题的解决思路。

现实生活中的对策现象是很多的，除了竞赛、战争等对策现象，还有许多其他方面的例子。例如在农业方面，在对大自然规律还没有完全掌握的条件下（如气候、自然灾害等），如何对施肥、选种、投资等进行决策，就是人与大自然之间进行的对策。又例如工厂企业之间的合作、兼并以及资金的投入等也是一种对策行为。不管是什么形式的对策现象，任何一个对策模型都必须包括以下三个基本要素。

1.局中人（Player）

参加对策的每一方称为局中人。通常用I表示局中人的集合，如果有n个局中人，则I={1,2,···,n}。一般要求局中人集合是一个至少包含两个元素的可列集合。如在“齐王赛马”中，局中人就是齐王和田忌。

对策中的局中人的概念是广义的。局中人除了可理解为个人外，还可理解为某一集体，如企业、公司、小组、国家等。当研究不确定的自然条件下进行某项与自然条件有关的生产决策时，就可把大自然当做一个局中人。另外，需要注意的是，在对策中总是假定每一个局中人都是“理性的”的决策者，即对任一局中人来讲，都是个人利益最大化或损失最小化的个体，或者说，不存在利用其他局中人决策失误来扩大自身利益的可能性。

2.策略集合（Strategy Set）

每个局中人在竞争的过程中，总期望自己取得尽可能好的结果。这样每个局中人都在想法挑选能达到目的的“方法”，我们把这种“方法”称为局中人的策略。如在乒乓球团体赛中运动员的出场次序就是一个策略。把一个局中人拥有的策略全体称为该局中人的策略集，如第i个局中人的策略集用Si表示。一般来说，每一局中人的策略集中至少应该包括两个策略。当每个局中人在一局对策中都在自己的策略集中选定一个策略后，这局对策的结果就被决定了。每个局中人所选定的策略放在一起称为一个局势。

在“齐王赛马”的例子中，如果用（上,中,下）表示以上马、中马、下马依次参赛这样一个次序，这是一个完整的行动方案，即为一个策略。可以得到，局中人齐王和田忌各自都有6个策略：（上,中,下）、（上,下,中）、（中,上,下）、（中,下,上）、（下,中,上）和（下,上,中）。(www.daowen.com)

要注意的是，策略是指局中人在整个竞争过程中对付他方的一个完整方法，并非指竞争过程中某一步所采用的局部行动。如“人不犯我，我不犯人；人若犯我，我必犯人”这是一个策略，而“不犯人”和“犯人”则是行动，不能称之为策略。同样在“齐王赛马”中，选择上马参赛是一个行动，而（上,中,下）这才是一个策略。

3.支付函数（Payoあ）

对策的结局用数量来表示，称为支付函数（或赢得函数），所以支付函数是定义在局势集合上的数值函数，用符合Hi表示局中人i的支付函数。

在“齐王赛马”的例子中，当齐王选择（上,中,下）这样的策略而田忌也选择（上,中,下）的策略时，齐王可以赢得3千金，而田忌会失去3千金，此时齐王的赢得是3，而田忌的赢得为-3。同样我们也可以得到其他局势下双方的赢得情况，如表9.1所示。

表9.1　“齐王赛马”问题的收益矩阵

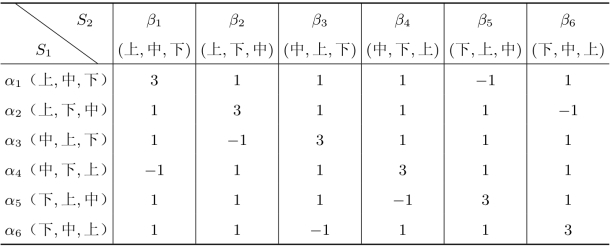
在表9.1中，局中人齐王的策略集为S1={α1,α2,···,α6}，局中人田忌的策略集为S2={β1,β2,···,β6}，把表9.1中的数值矩阵

称为局中人齐王的支付函数。

一般而言，当上述三个基本因素确定后一个对策模型也就确定了。