目前存在着许多的多属性决策方法，而且这些方法还在不断地发展中。这里介绍两种最为常用的有效方法。

1.简单加权和法

加权和法的求解步骤比较简单，它利用不同方案各属性的加权和作为方案排序的依据，其具体步骤如下：

(1)选择前述的适当方法对各属性值进行规范化处理。假设规范化处理后，方案i的属性j的规范化值为yij。

(2)确定各属性的权重系数wj(j=1,2,···,n)。

(3)计算各方案的属性值加权和，即令

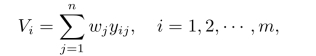
根据Vi值的大小对方案进行排序，确定决策结果。

如前述的供应商选择的决策（见表8.20）中，按上述步骤可以得到如表8.23所示的计算结果。

表8.23　供应商选择决策

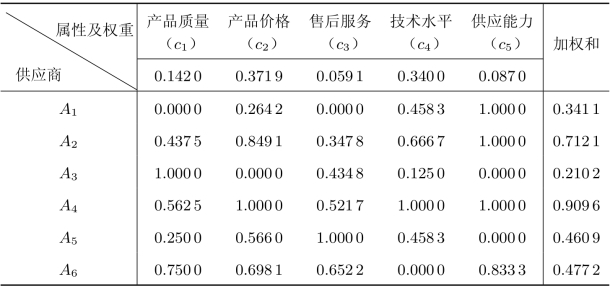
由此得到各供应由优到差的排序为A4≻A2≻A6≻A5≻A1≻A3。

加权和法由于简单、直观，成为最为常用的多属性决策方法。采用加权和法的关键在于确定指标体系，并且设定各属性的权重系数。但在使用加权和法时实际上隐含着如下的基本假设：

(1)属性（指标）体系呈树状结构；

(2)每个属性的边际值是线性的，即优劣与属性值大小成比例，每两个属性值都是相互独立的；

(3)属性间应具有完全可补偿性，即一个方案的某属性无论多差都可用其他相对较好的属性进行补偿。

事实上，以上假设往往并不成立。首先，指标体系通常是网状的。其次，属性的边际值常常是局部线性的，甚至有时最优值为给定区间（或点）；不同属性间的值极难满足其独立条件，即使满足独立性，有时也极难验证其满足。而且属性间通常只是部分地、有条件地可补偿。所以，使用加权和法要十分谨慎。

2.TOPSIS方法

TOPSIS为接近理想点法（Technique for Order Preference by Similarity to Ideal Solution）的缩写。其基本思想为：假想一个理想方案和一个负理想方案，然后分别确定各方案与理想方案和负理想方案的距离，与理想方案最近且与负理想方案最远的方案为最优方案。所以TOPSIS是一种基于距离的方案排序方法，该方法所使用的距离为（赋权后的）欧氏距离。TOPSIS方法的具体步骤如下：(www.daowen.com)

(1)用向量规范化方法求得规范化决策矩阵。设多属性决策问题的决策矩阵为X=(xij)，规范化决策矩阵为Y=(yij)，则

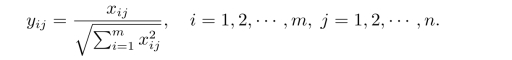
(2)构成赋权规范矩阵V=(vij)。若各属性的权重向量为w=(w1,w2,···,wn)T，则

(5)计算各方案的相对接近度，令

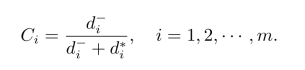
(6)根据相对接近度Ci值对各方案进行排序。

以前述供应商选择问题为例，首先根据表8.19的数据，利用向量规范化方法得到规范后的矩阵如表8.24所示。

表8.24　规范化处理后的数据

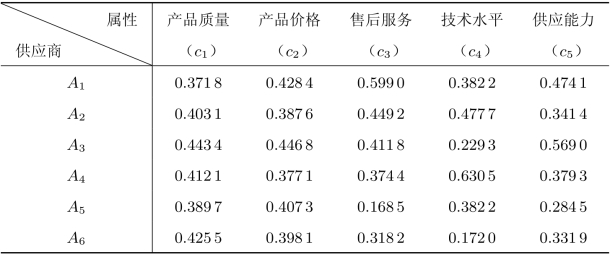
若各属性的权重为w=(0.142 0,0.371 9,0.059 1,0.340 0,0.087 0)T，则得到赋权后的规范矩阵如表8.25所示。

表8.25　赋权规范化处理后的数据

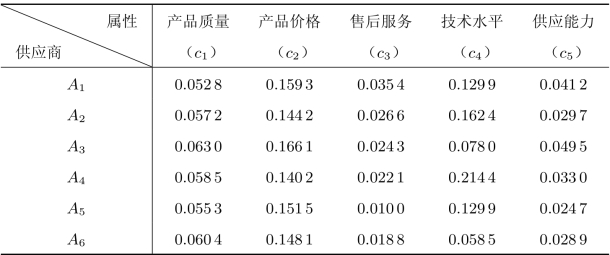
在5个考察属性中，产品质量、技术水平、供应能力为效益型属性，产品价格与售后服务为成本型属性，所以得到理想方案和负思想方案分别为然后分别计算各方案到理想方案与负理想方案的距离，以及各方案的相对接近度。结果如表8.26所示。

表8.26　各方案分别到理想方案与负理想方案的距离及相对接近度

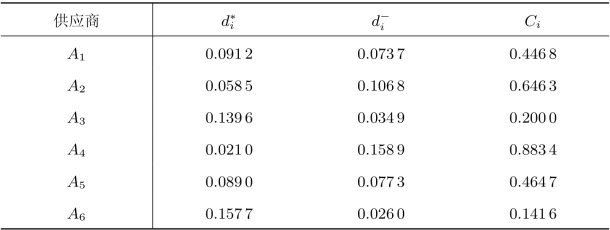
由此得到各供应商的排序为A4≻A2≻A5≻A1≻A3≻A6。