决策者为了在具有多个属性的备选方案中作出选择，通常需要设定不同属性的权重以反映决策者在方案选择时的偏好，所以权重反映了：（1）决策者对目标属性的重视程度；（2）各目标属性值的差异程度；（3）各目标属性值的可靠程度。权重应当综合反映这三种因素的作用，而且通过权重可以使用各种方法将多属性决策问题化为单属性问题求解。

目前存在着多种权重确定的方法，但基本上可分为主观赋权法和客观赋权法两类。

主观赋权法是指人们依照经验主观确定属性权重。在赋权的过程中充分发挥专家作用，利用专家的知识、经验来确定权数。所以，这类方法实际上是专家调查、专家征询法，典型方法包括头脑风暴法、Delphi法等。这类方法的主要缺点是主观随意性较大，权重的确定与专家的经验、知识水平等有着较大的关联性。

客观赋权法是指通过科学的方法对客观资料进行整理、计算、分析而得到的权重，避免了人为因素和主观因素的影响。这类方法来源于客观实际数据，有较强的客观性，其权重的准确性取决于提供数据的准确程度。

下面介绍几种较为常用的方法。

1.AHP法

在多属性决策中，对属性权重的确定也可以采用前述的AHP法。根据决策者对各个属性的相对重要性的判断得到判断矩阵后，可以利用前面的AHP法计算各属性的权重。

如前述的供应商选择的决策问题中，如果对5个属性的相对重要性作两两比较得到如下的判断矩阵：

利用前述的方根近似法，求得权重向量为

一致性判断系数CR=0.051 29<0.1，判断矩阵满足一致性要求。

2.最小平方和法

最小平方和法是由Cku、Kalaba和Spingarn三人于1979年提出的，其基础还是利用决策者的判断矩阵（如Saaty矩阵），而原理比Saaty的特征向量法要简单。

上述优化问题可以通过构造拉格朗日函数L求解，

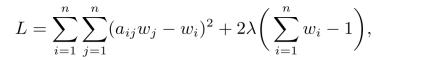
其中λ为拉格朗日乘子。

将L对wl(l=1,2,···,n)求偏导数，并令其为0，得到n个代数方程：

而其他元素

由此即可解得权重向量w。

仍以前述供应选择问题为例，假设判断矩阵A为

根据(8.5),(8.6)可求得系数矩阵B如下：

也即有

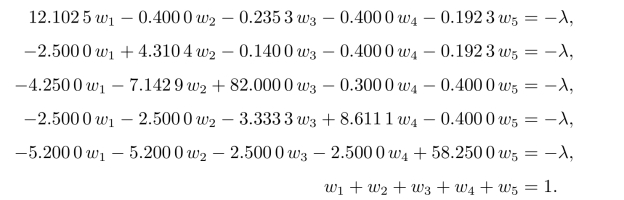
由此可解得w=(0.142 0,0.371 9,0.059 1,0.340 0,0.087 0)T。

3.熵权法

现代信息论的奠基人C.E.Shannon在1941年首先提出了信息熵的概念，解决了对信息的量化度量问题。按照信息论基本原理的解释，信息是系统有序程度的一个度量，熵是系统无序程度的一个度量，两者绝对值相等，但符号相反。因此，根据这一性质，可以利用多属性决策中各属性的固有信息，计算其熵值。如果指标的信息熵越小，则该指标提供的信息量越大，在多属性决策中所起作用理当越大，权重就应该越高；反之，如果指标的信息熵越大，则该指标提供的信息量越小，其信息的作用就越小，权重也应该越小。(www.daowen.com)

如果某个离散随机变量X的概率分布为pj=P{X=xj}(j=1,2,···,n)，则该随机分布所包含的信息量为

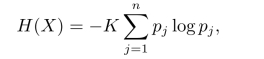
这就是信息熵的计算公式，其中K为一正常数，它的值主要依赖于对数取不同的底数。当X的概率分布为均匀分布时，H(X)取得最大值log n，即均匀分布的熵最大。

下面利用信息熵的概念来进行权重的确定。假设多属性决策矩阵为

其中Ai(i=1,2,···,m)表示m个备选方案，Xj(j=1,2,···,n)表示每个方案具有n个属性，xij表示不同方案在不同属性下的取值。用

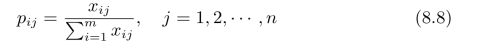
表示第j个属性Xj下第i个方案Ai的贡献度，这种贡献度可以说是包含有一种信息内容，因此可以用Ej来表示所有方案（m个方案）对属性Xj的贡献总量：

从(8.9)可以看出，当某个属性下各方案的贡献度趋于一致时，Ej趋于1，特别是当全相等时，也就可以不考虑该目标的属性在决策中的作用，也即此时属性的权重为零。

如现有一决策矩阵为

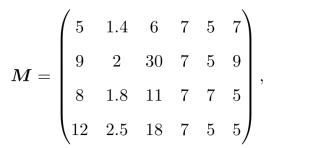
则第4个属性的权重为0。

这样可以看出属性值的权重由所有方案差异大小来决定权系数大小，为此可定义dj为第j个属性下各方案贡献度的一致性程度：

则各属性权重可表示为

当dj=0时，第j个属性可以剔除，其权重为零。

如果决策者事先已有一些经验的主观估计权重λj，则可借助上述的wj来对λj进行修正，即

熵值法的最大特点是利用决策矩阵所给的信息来计算权重，而没有引入决策者的主观判断。

例8.7某人在购买汽车的决策问题中，考虑了4种车型以及油耗、功率、费用、安全性、维护性、操纵性等6个属性，得到相应的决策矩阵如下：

首先利用(8.8)计算出贡献度pij，如表8.21所示。

表8.21　购买汽车决策问题的贡献度pij

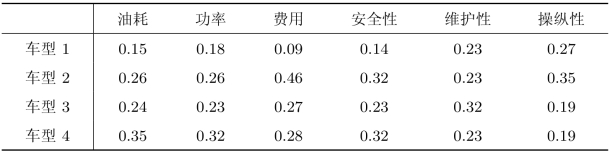
各属性的熵值Ej,dj及确定的权重wj如表8.22所示。

表8.22　购买汽车决策问题的属性熵值及权重确定

如果决策者事先主观给出的各属性权重为

则经修正后可得w′=(0.07,0.03,0.68,0.14,0.03,0.05)T。