由于属性数据的量纲、数据方向、数量级等方面的不一致，为了进行备选方案的综合比较，在进行多属性决策时首先需要对属性数据进行规范化处理，常用的方法如下：

1.线性变换

令原始属性值矩阵为X=(xij)，变换后的矩阵为Y=(yij)。线性变换方法为

经过线性变换后，yij为无量纲的，而且对于效益型属性和成本型属性最优值均为1，而且越接近1越优。需要说明的是，上述变化中效益型属性是线性变换，而成本型属性是非线性的变换。

2.0-1变换

属性值经过线性变换后最优值为1，但最差值一般不为0；若最差值为0，最优值往往不为1。为了使每个属性值变换后的最优值为1且最差值为0，可以使用0-1变换来实现。其变换方法为

3.向量规范化

向量规范化方法对于成本型属性和效益型属性都使用相同的方法，即(www.daowen.com)

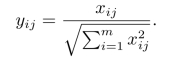
这种变换方法从属性值的大小上无法分辨属性的优劣，它的最大特点是规范化后各方案的同一属性值的平方和为1。

4.中间型属性数据的变换

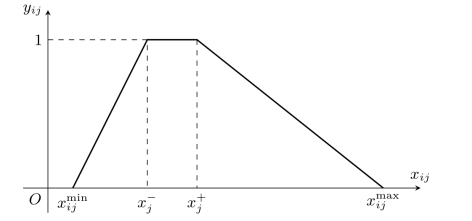
图8-10　中间型属性数据的变换

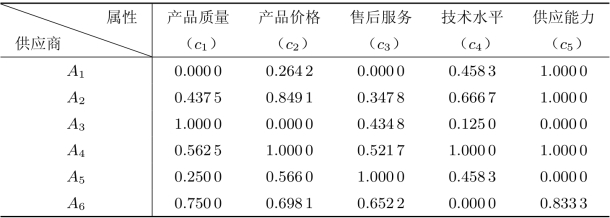
在例8.6中，产品质量、技术水平为效益型数据，产品价格和售后服务为成本型数据，供应能力为中间型数据（假设最优区间为[180,250]），则利用前述0-1变换和中间型数据变换的规则得到变化后的属性决策表为表8.20。

表8.20　变换后的属性决策表