一般情况下，在AHP法中计算判断矩阵的最大特征值与特征向量并不需要太高的精度，所以一般采用近似方法进行计算，其中最为常用的是方根法。AHP法的计算步骤如下：

(1)根据层次模型，构建不同层次的判断矩阵。设有目标层A、准则层C={C1,C2,···,Ck}、方案层P={P1,P2,···,Pn}构成的典型层次模型（当层次增多以后，计算过程类似）。则可以得到一个A-C判断矩阵A和k个C-P判断矩阵Ci，如下：

(2)利用方根法求各判断矩阵的特征向量及最大特征值。方根法的具体过程如下：

计算判断矩阵每行所有元素的几何平均值：

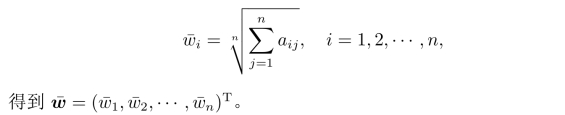
将得到的¯wi作归一化处理，即计算

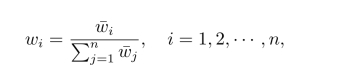
得到w=(w1,w2,···,wn)T即为所求特征向量的近似值，也就是各因素的相对权重。

计算判断矩阵的最大特征值

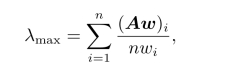
其中(Aw)i为向量Aw的第i个元素。

(3)根据(8.1)和(8.2)式计算判断矩阵一致性指标，检验其一致性。

(4)进行组合权重计算。若目标层A对准则层C的相对权重为

准则层的各准则Ci对方案层n个方案的相对权重为

(www.daowen.com)

表8.15　权重组合计算

下面我们对前述风险投资问题进行AHP法的计算。根据决策者对4个准则对于实现总目标的重要性，建立A-C层的判断矩阵，得到

根据方根法的计算过程，得到4个准则的相对权重为

其中最大特征值、一致性指标和一致性检验指标分别为

说明判断矩阵满足一致性要求，可以作为4个准则的相对权重。

按照同样的方法，可以得到Ci-P层的相对权重，如表8.16所示。

表8.16　Ci-P层的相对权重

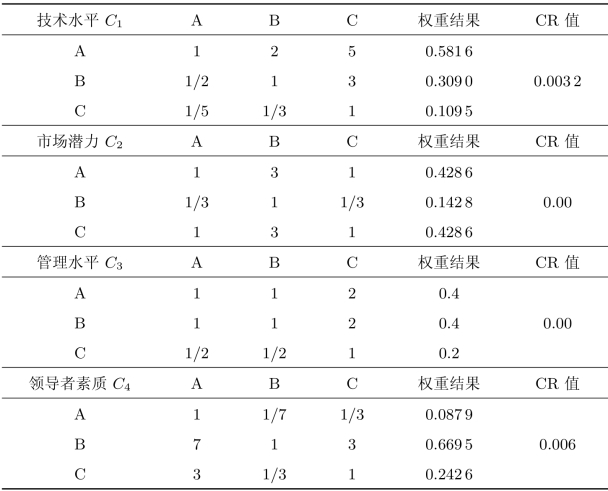
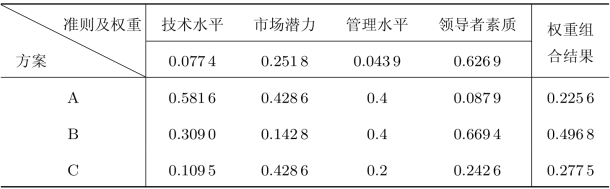
最后，根据表8.15进行合成以确定每个方案的得分，从而进行方案排序，结果如表8.17所示。从表8.17可以看出，项目B的综合评价最好，所以最佳选择是项目B，其次是项目C，最后是项目A。

表8.17　权重组合计算