用期望值法进行决策分析求得的最优方案是期望报酬值最大意义下的方案，它只能保证在统计意义上达到预期目标，即当决策问题多次反复出现时，用期望收益值最优来指导决策效果较好。在具体一次实践中，期望收益值不一定是实际报酬值。

图8-7　序列决策示例

例如，某公司有笔闲置资金，有两种可供选择的投资方案a1和a2。方案a1为投资到某种风险基金，根据往年的收益情况来看，该基金盈利的概率为0.7，盈利后的收益为10万元；基金亏损的概率为0.3，亏损金额为3万元。方案a2为银行储蓄，收益为5万元。显然这是一个风险型决策问题，根据最大期望收益准则容易得到最优方案为a1，获得6.1万元的期望收益。这是一个统计意义上的期望值，如果基金盈利，选择此方案的实际收益为10万元，多于期望收益和确定收益（银行储蓄的收益）。但如果亏损，则实际收益为-3万元，低于期望收益和确定收益。这样看来，追求期望收益值是有风险的，而不同的决策者对待风险的态度是不同的。效用理论为描述决策者对待风险的态度提供了方法。

简单而言，一个决策问题中所有可能收益的集合称为收益集，记为R。如果一个决策者认为R中的r1优于r2，用r1≻r2或r2≺r1表示；如果他认为r1和r2是相当的，记为r1～r2。

效用函数是定义在收益集R上的一个实函数u(r)，它满足这样的一些基本要求：当r1≻r2时，有u(r1)>u(r2)；当r1～r2时，存在u(r1)=u(r2)。效用函数反映了决策者对r的偏好程度，对于同一决策问题，不同决策者的效用函数可能不同，从而反映了不同决策者对待风险的态度。

这样，前述的风险型决策问题可以首先根据不同决策者的效用函数，将决策的收益值转化为效用值后，再利用效用值的期望值进行决策，即不同方案的期望效用值为

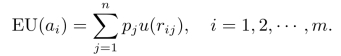
根据效用函数的曲线形态，通常可以把决策划分为三种类型，如图8-8所示。

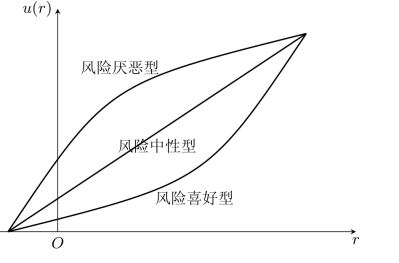
图8-8　效用曲线的基本形态

风险中性型决策者的效用曲线为一条直线，他认为收入金额的增长与效用值的增长成等比关系；风险厌恶型决策者的效用曲线是一条上凸曲线，他对损失金额愈多愈敏感，相反地对收入的增加比较迟钝，即他不愿意承担损失的风险；风险喜好型的决策者效用曲线是一条下凸曲线，他对损失金额比较迟钝，相反地对收入的增加比较敏感，即他可以承受损失的风险。

在决策风险时通常使用决策者风险厌恶的假设，因为一般情况下决策是尽量地避免承担风险。常用的效用函数有

(1)线性函数u(r)=c1+a1(r-c2)；

(2)指数函数u(r)=c1+a1(1-ea2(r-c2))；

(3)双指数函数u(r)=c1+a1(2-ea2(r-c2)-ea3(r-c3))；

(4)指数加线性函数u(r)=c1+a1(1-ea2(r-c2))+a3(r-c3)；(www.daowen.com)

(5)幂函数u(r)=a1+c1(r-a2)a3；

(6)对数函数u(r)=c1+a1 ln(c2r-c3)。

下面通过一个实例来说明如何利用期望效用值进行决策分析。

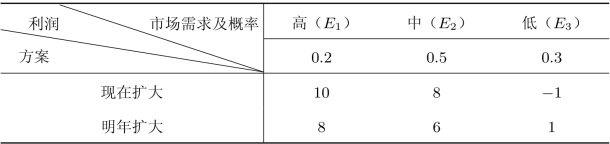
例8.5(效用函数的应用)某工厂正考虑是现在还是明年扩大生产规模的问题。由于可能出现的市场需求情况不一样，预期利润也不同。已知市场需求为高、中、低的概率及不同方案时的预期利润（单位：万元）如表8.12所示。对该厂来说损失1万元效用值为0，获利10万元效用值为100，对以下事件效用值无差异：

(1)肯定得8万元或0.9概率得10万元和0.1概率失去1万元；

(2)肯定得6万元或0.8概率得10万元和0.2概率失去1万元；

(3)肯定得1万元或0.25概率得10万元和0.75概率失去1万元。

试用效用值决策，并与利用实际盈利额时的决策进行比较。

表8.12　效用函数的应用

解根据题意可知，u(-1)=0，u(10)=100，

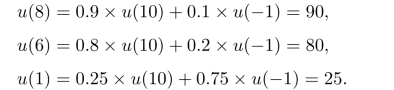
这样，企业选择现在扩大生产规模时的期望效用值和期望收益值分别为

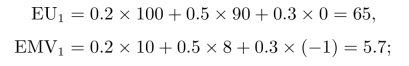
企业选择明年扩大生产规模时的期望效用值和期望收益值分别为

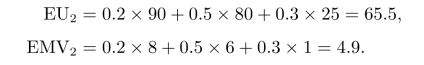
所以，根据最大期望效用准则企业应该选择明年扩大生产规模，根据最大期望收益准则企业应选择现在扩大生产规模。由此可见，把收益作为决策目标和把效用值作为决策目标，其结果可能是不同的。一般利用效用函数进行决策分析更能反映决策者的主观愿望。