有些决策问题当进行决策后产生一些新情况，并需要进行新的决策，接着又有可能出现一些新情况，又需要进行新的决策，这种需要根据情况变化连续做出决策的问题称为序列决策。对于序列决策问题，使用的基本规则还是将期望收益作为方案选择的依据，通常使用决策树进行序列决策问题的分析。

例8.4(序列决策)某市郊工厂为解决用水有两个可供选择的方案：

(1)铺设连接城市自来水网的管道，需投资11 000元；

(2)就地挖井，但因井位选择上的差别，需要投资额可能为10 000元（概率0.3）、11 000元（概率0.3）、12 000元（概率0.4）。

无论铺设管道或挖井，均能解决工厂规划期内的用水问题。为了确定一个较好的井位，可请当地水文组帮助选择，但需花费150元。又水文组提供的意见仅是在某一地点是否适宜挖井。据资料统计，在过去类似挖掘投资为10 000元的井中，水文组认为宜挖的占80%，认为不宜挖的占20%；在挖掘投资为11 000元的井中，水文组认为宜挖的占60%，不宜挖的占40%；在挖掘投资为12 000元的井中，水文组认为宜挖的占20%，不宜挖的占80%。试用决策树法分析该厂解决用水问题应采用哪一种方案；若该厂决定挖井，是否需要求助地质水文组帮助选择井位。

解假设T1表示需投资10 000元，T2表示需投资11 000元，T3表示需投资12 000元，E1表示水文组意见为宜挖井，E2表示水文组意见为不宜挖井。根据问题描述可以得到P(T1)=0.3，P(T2)=0.3，P(T3)=0.4，而且有(www.daowen.com)

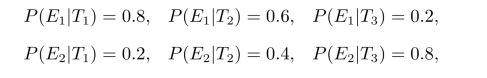
这样可求得P(E1)=0.5，P(E2)=0.5，以及

决策树分析如图8-7所示。

决策结果为：该厂应请水文地质队帮助选择宜挖井的地点。如果水文地质队提出宜挖井时，则挖井；如果水文地质队提出不宜挖井时，则应采用与城市自来水网连接的方案。