在决策模型中自然状态的概率和损益值往往由估计或预测得到，不可能十分准确，此外实际情况也在不断发生变化。所以在风险型决策中，方案的灵敏度分析就显得十分重要了。所谓灵敏度分析就是分析决策所用的数据在什么范围内变化时，原最优决策方案仍然有效。通常是对自然状态发生的概率进行灵敏度分析，也就是考虑自然状态发生概率的变化如何影响最优方案的选择。自然状态概率发生变化时，最优方案也发生了相应变化，这时的概率称为转折概率。下面通过一个实例来说明概率灵敏度分析的一般思路。

例8.3(灵敏度分析)某决策问题的相关数据如表8.11所示。

表8.11　决策问题的灵敏度分析

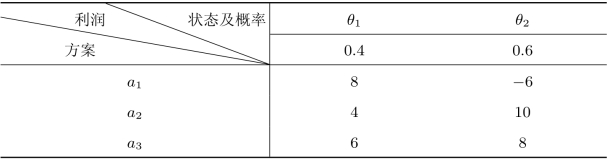
解容易知道，当前概率条件下，方案a1,a2,a3的期望收益分别为-0.4,7.6和7.2，所以现在的最优决策为选择方案a2。

为了研究概率变化对决策方案选择的影响，现假设θ1发生的概率为p1，则θ2发生的概率为1-p1，由此得到不同方案的期望收益分别为

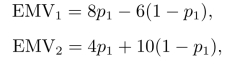
(www.daowen.com)

为了便于分析，将这三个方案的期望收益与状态概率的关系绘制在图8-6中。由图8-6可以发现，三条期望收益曲线相交于三点。为保证期望收益最优，应该保证在不同概率下选择最高的期望收益曲线。所以可以得到

当0≤p1≤0.5时，EMV2最大，此时的最优决策方案为a2；

当0.5≤p1≤0.875时，EMV3最大，此时的最优决策方案为a3；

当0.875≤p1≤1时，EMV1最大，此时的最优决策方案为a1。

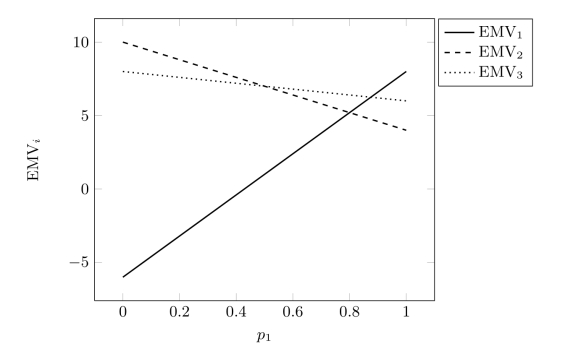
图8-6　决策问题的灵敏度分析图

上述分析中，p1=0.5和p1=0.875为概率转折点。事实上，上述的灵敏度分析只是一个简单的基本思路，当方案数和状态数增多后，灵敏度分析就会越复杂。