时间-费用优化指在进行网络优化时，研究如何使得工程完工时间短、费用少。具体而言，一般包括两方面的内容：一是在保证既定的工程完工时间的条件下，所需要的费用最少；二是在限制费用的条件下，工程完工时间最短。

在进行一项工程时，所涉及的费用可以划分到两大类型中去：直接费用或间接费用。

直接费用包括直接生产工人的工资及附加费，设备、能源、工具及材料消耗等直接与完成工序有关的费用。为缩短工序的作业时间，需要采取一定的技术组织措施，相应地要增加一部分直接费用，在一定条件下和一定范围内工序的作业时间越短，直接费用越多。

间接费用包括管理人员的工资、办公费用等，该费用通常按施工时间长短分摊，在一定生产规模内，工序作业时间越短，分摊的间接费用就越少。

所以，工程（工序）的总费用由上述两种费用构成，它们与工程（工序）完工时间的关系如图7-16所示。

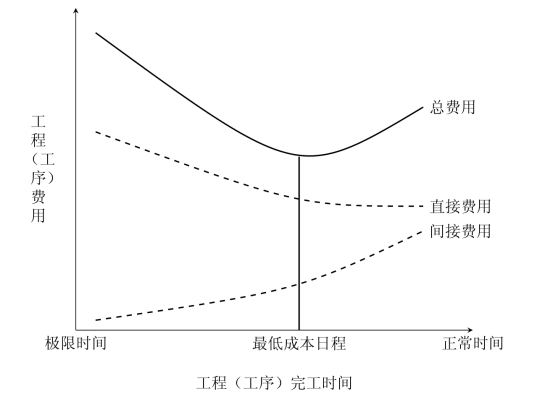
图7-16　网络费用类型及其与工程完工时间的关系

在图7-16中，正常时间是指在现有的生产技术条件下，由各工序的作业时间所构成的工程完工时间。而极限时间是指为了缩短各工序的作业时间而采取一切可能的技术组织措施之后，可能达到的最短作业时间和完成工程的最短时间。

在进行时间-费用优化时，需要计算在采取各种技术组织措施之后，工程的不同的完工时间所对应的工序总费用和工程所需要的总费用。使得工程费用最低的工程完工时间称为最低成本日程。在进行网络计划与优化时，无论是以降低费用为主要目标，还是以尽量缩短工程完工时间为主要目标，都要计算最低成本日程，从而提出时间-费用的优化方案。

网络的时间-费用优化是一个非常繁琐、计算量较大的工作，下面仅以一个实例来说明网络时间-费用优化的基本思路。

例7.6(时间-费用优化)已知某项工程的相关资料如表7.5所示，求该工程的最低成本日程。(www.daowen.com)

解首先绘制网络图，按工序的正常作业时间计算相关时间参数，确定工程的关键路线，结果如图7-17所示。

表7.5　某项工程的相关资料数据

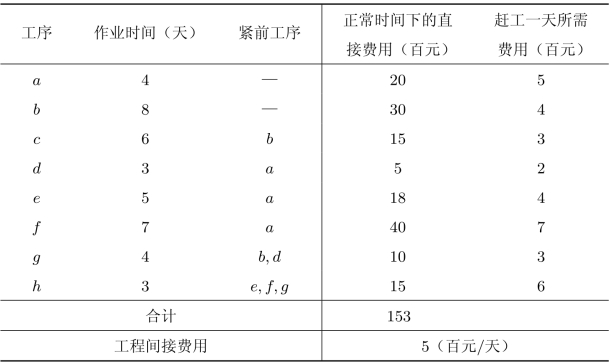
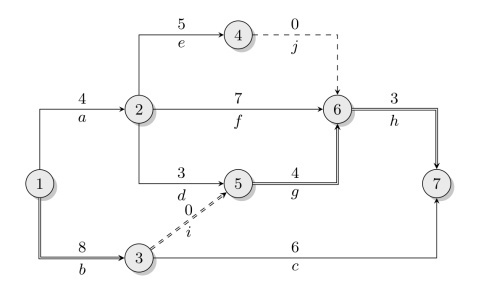
图7-17　某工程的网络图

该工程的关键路线为b→g→h（图7-17中以双线表示），工期为15天，当前工程的总费用为153+5×15=228百元。

为了缩短工程的工期，必须缩短关键路线。对于关键工序h，由于赶工作业一天的费用6百元超过了工程间接费用5百元/天，所以缩短工序h是得不偿失的。再看b,g这两道工序，它们的单位赶工费用都低于单位工程间接费用，所以赶工作业是可行的。但是要注意的是，它们赶工作业只能缩短一天工期，不然a→f→h就成为了关键路线。若b,g赶工作业超过一天，但工程的工期却只能缩短一天，这样多赶工的时间是不会缩短间接费用，却只增加了直接费用，是不可行的。进一步，b缩短一天增加的费用为4，g缩短一天增加的费用为3，所以g缩短一天的作业时间更优。这样得到的工程工期为14天，总费用为228-5+3=226百元。如图7-18所示。

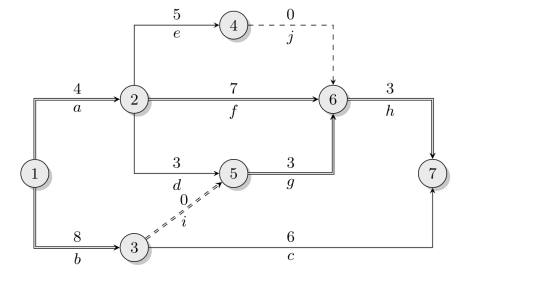
图7-18　某工程的工期-成本优化结果

事实上，在图7-18中，关键路线有两条：a→f→h和b→g→h，若还要做缩短工程工期的方案，则有：(1)单独缩短h的作业时间；(2)同时相同缩短a,f和b,g的作业时间。读者可自行验证这两种方案都是不可行的。