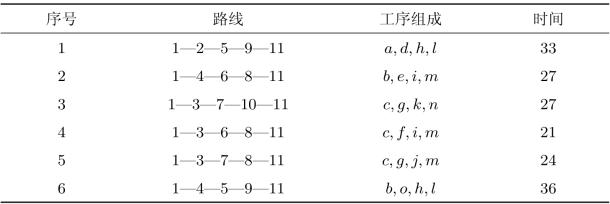
在一个网络中，从始点开始连续不断地到达终点的一条通路称为路线。通常这样的路线有很多，在各条路线上完成各个工序的时间之和也不完全相等，这些时间表示既定路线的时间长度。以图7-2为例，该网络中存在的路线及其时间长度如表7.2所示。

从表7.2中可以发现，不同路线都从工程开始走到了工程结束，但时间不同。为了保证整个工程的完成，应该选择最长的时间作为工程的工期。完成各个工序需要时间最长的路线称为关键路线或主要矛盾线，组成关键路线的工序称为关键工序。如图7-2中，路线1-4-5-9-11为关键路线，b,o,h,l为关键工序，完成整个工程的工期为36。

表7.2　网络中不同的路线及其时间长度

通过上述简单的分析可以发现：

(1)要缩短工程的工期，需要缩短关键工序所需的时间。

(2)关键路线是相对的，可以变化的。如采取一定措施后，原来关键工序所需时间得到缩减，这时原来的非关键工序有可能就成为了关键工序，从而使得关键路线发生变化。

由此可见，在网络图中找出关键路线是编制网络计划的基本思想，但是关键路线的确定依赖于工序所需时间以及相关的时间参数的计算。所以，进行网络计划与优化的前提是网络时间参数的计算。

通常网络时间参数包括三种：工序持续时间、事项时间和工序时间，下面分别展开介绍。

1.工序持续时间（Tij）

工序持续时间是指网络图中完成某工序时所需的时间，通常用Tij来表示。对于工序持续时间的确定通常有如下两种方式：

(1)确定型：每项工序持续时间存在着一个确定的值。如在具备工时定额和劳动定额的任务中，工序持续时间可依据相关定额资料进行确定，或者可依据相关统计资料，根据统计分析结果进行确定。如每个车床完成加工一个螺丝的时间、流水线上完成某项工作的时间、汽车装配线安装车门所需的时间等。

(2)概率型：对于一些新的工作，如开发性、试制性的工作，往往不具备相关的定额数据资料，当工序的持续时间难以准确估计时，可以采用三点时间估计法来确定工序的持续时间。利用三点时间估计法时，工序持续时间的估计值为

估计的方差为

其中a为最快可能完成时间（乐观时间），m为最可能完成时间（正常时间），b为最慢可能完成时间（悲观时间）。

2.事项时间

(1)事项的最早时间（TE(j)）

若事项j为箭尾事项，则该事项的最早时间TE(j)表示以它为始点的各工序最早可能开始的时间；若事项j为箭头事项，则TE(j)表示以它为终点的各工序的最早可能完成时间。所以，TE(j)应等于从始点事项到该事项的最长路线上所有工序的持续时间总和。具体计算时，可按下述递推公式按照编号从小到大顺序逐个计算。设网络初始编号为1，则

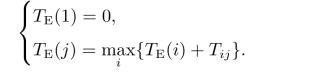
例7.3(事项最早时间的计算)试计算图7-2所示网络中各事项的最早时间。

解图7-8中我们用方框加数字表示各事项的最早时间。计算时，从初始编号开始，从左往右，依次计算到达某点的路线的时间最大值，即为该事项的最早时间。

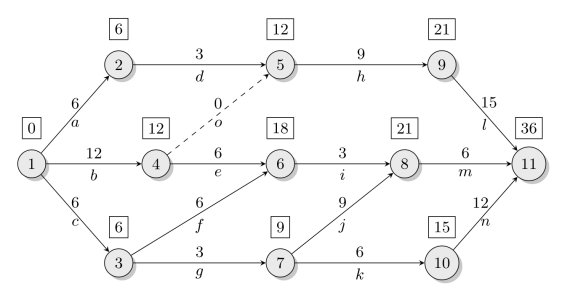
图7-8　事项最早时间的计算

(2)事项的最迟时间（TL(i)）

事项的最迟时间表示在不影响任务总工期的条件下，以它为始点的工作（i为箭尾事项）最迟必须开始的时间，或以它为终点的各工作（i为箭头事项）最迟必须完成的时间。由于一般情况下我们都把任务的最早完工时间作为任务的总工期，所以事项最迟时间的计算公式为

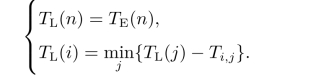
可见，该过程也是一个递推计算，但与最早时间的计算相反，按编号从大到小依次计算到达某点的最小值。

例7.4(事项最迟时间的计算)试计算图7-2所示网络中各事项的最迟时间。

解图7-9中我们用圆圈加数字表示各事项的最迟时间。计算时，首先让TL(11)=TE(11)，然后从右往左，依次计算到达各点的最小时间即可。

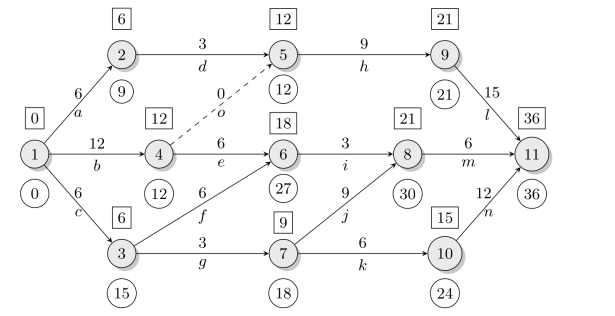
图7-9　事项最迟时间的计算(www.daowen.com)

3.工序时间

工序时间是在前述工序持续时间、事项时间参数的基础上通过计算得到的，包括工序的最早开始时间、最早结束时间、最迟结束时间、最迟开始时间、总时差、自由时差等6个参数，它们是确定网络关键路线和网络优化的基础和依据。

(1)工序的最早开始时间（TES(i,j)）

任何一个工序都必须在其紧前工序结束后才能开始，所以紧前工序的最早结束时间即为工序的最早可能开始时间，称为工序的最早开始时间，用TES(i,j)表示，它等于该工序箭尾事项的最早时间，即TES(i,j)=TE(i)。

(2)工序的最早结束时间（TEF(i,j)）

该参数表示工序最早可能结束时间，所以它等于工序的最早开始时间加上该工序的持续时间，即TEF(i,j)=TES(i,j)+Tij。

(3)工序的最迟结束时间（TLF(i,j)）

该参数表示在不影响工程最早结束时间的条件下，某项工序最迟必须结束的时间，所以它应等于该项工序的箭头事项的最迟时间，即

(4)工序的最迟开始时间（TLS(i,j)）

该参数表示在不影响工程最早结束时间的条件下，工序最迟必须开始的时间，所以它等于该项工序的最迟结束时间减去该项工序的持续时间，即

(5)工序的总时差（TF(i,j)）

该参数表示在不影响工程最早结束时间的条件下，工序最早开始（或结束）时间可以推迟的时间，即

(6)工序的自由时差（FF(i,j)）

该参数表示在不影响紧后工序的最早开始时间的条件下，某工序最早结束时间可推迟的时间，所以该工序的自由时差为

上述6个工序时间参数是进行网络分析与优化的基础，它们之间的关系如图7-10所示。

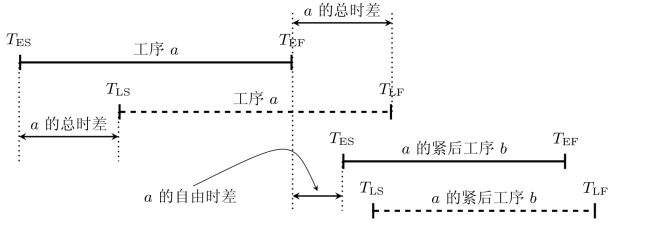
图7-10　工序时间参数的关系

在一个工程网络中，若某项工序的总时差为零，则意味着该项工序的开始和结束时间没有一点活动的余地。由这些工序所组成的线路就是网络中的关键路线，这些工序就是关键工序。

例7.5(工序时间参数的计算)试计算图7-2所示网络中各工序的时间参数，并确定网络的关键路线与关键工序。

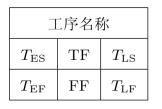
解根据前述网络中事项时间的计算结果，结合工序时间参数的定义，容易得到各工序的时间参数。为清晰起见，我们对某项工序采取如下的表格来表示工序的6个时间参数：

各工序时间参数计算结果如图7-11所示。

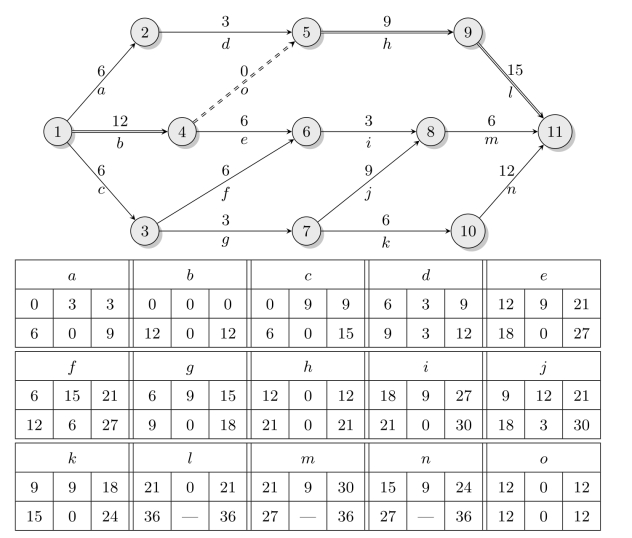
图7-11　工序时间参数的计算

根据计算结果，工序b,o,h和l的总时差为0，所以这些工序为关键工序，从而形成的网络关键路线为1→4→5→9→11（在图7-11中以双线标出）。

需要说明的是，前面的例子均是以双节点网络图为基础展开相关参数计算的说明，单节点网络图中时间参数的计算过程是类似的，就不再重复。

根据网络时间参数的计算结果，通常将网络计划体现在横道图（或称甘特图）中。横道图将各工序的时间安排体现在一张以时间为横轴的图中，可以清楚了解工序之间的逻辑关系以及工序的时间参数。如前述例子的计算结果的横道图如图7-12所示。

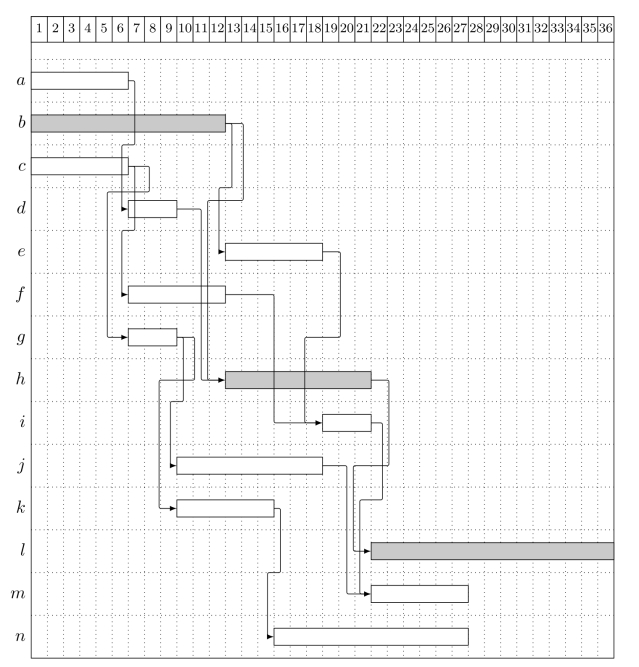
图7-12　网络的横道图