Dijkstra标号法只适用于无负权网络的最短路问题。对有负权网络该算法是失效的。如图6-28所示的赋权有向图中，如果用Dijkstra方法，可得到从v1到v3的最短距离为2，这显然不对，因为从v1经v2到达v3的最短距离为-4。

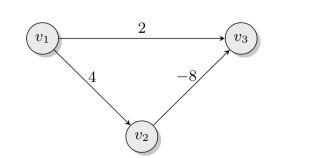
图6-28　有负权网络的最短路问题

在存在负权的网络中，不妨设从任一点vi到任一点vj都有一条弧，如果(vi,vj)/∈A，则添加弧(vi,vj)，并令wij=+∞。显然，从vs到vj的最短路总是从vs出发，沿着一条路线到达某个点vi，再沿弧(vi,vj)。由于最短路中某一点到终点的最短路也是沿着这条路线的，即从vs到vi的这条路线必定是从vs到vi的最短路，所以d(vs,vj)必定满足下述方程：为了求得这个方程的解，可用如下递推公式：

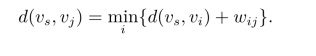
开始时，令d(1)(vs,vj)=wsj,j=1,2,···,p。对t=2,3,···，

若进行到某一步（第k步），对所有j=1,2,···,p都有

则{d(k-1)(vs,vj)}j=1,2,···,p即为vs到各点的最短路的权。(www.daowen.com)

例6.5(有负权网络的最短路)求解图6-29中vs到vt的最短路。

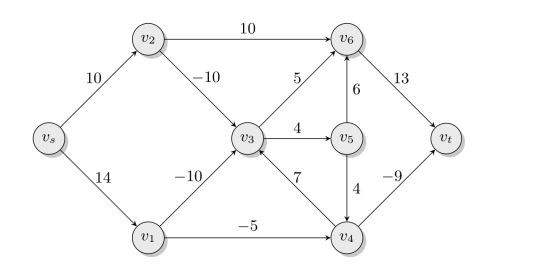
图6-29　负权网络的最短路问题

解为了实现上述的递推过程，我们用表格的方式进行运算，具体过程体现于表6.1中。

表6.1　有负权网络最短路的求解过程

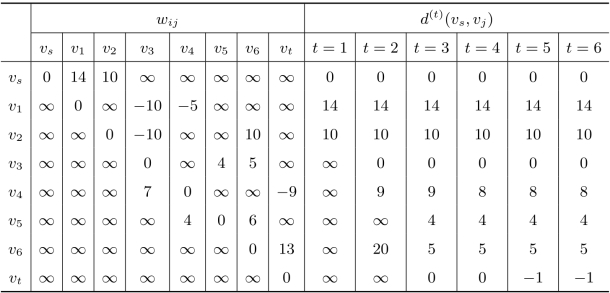
注意到，t=6所在列与t=5所在列的距离相同，所以t=5所在列即为vs出发到各点的最短距离，具体路线如图6-30所示。

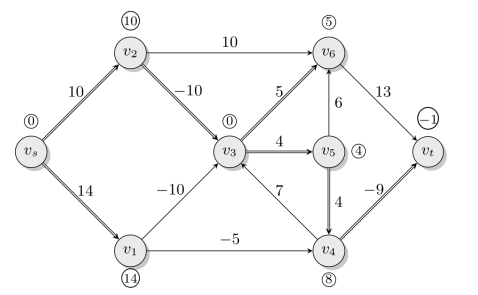
图6-30　有负权网络的最短路问题